Série entière
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Steve17
- Messages: 5
- Enregistré le: 17 Nov 2023, 14:54
-
 par Steve17 » 28 Fév 2024, 12:58
par Steve17 » 28 Fév 2024, 12:58
Bonjour à tout le monde, svp j'aimerais avoir de l'aide sur cet exercice si possible.. Merci d'avance
On donne la série

1) Pour quelle valeur de x la série converge-t-elle ?
2) Calculer lorsqu'elle existe la somme S(x)=
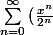})
3)Quel est le rayon de convergence et la somme de série entière de terme général
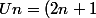(x^n))
Modifié en dernier par
Steve17 le 28 Fév 2024, 16:03, modifié 1 fois.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 28 Fév 2024, 13:04
par Ben314 » 28 Fév 2024, 13:04
Salut,
Cours de Lycée (suites géométriques) : pour tout
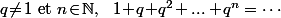
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Steve17
- Messages: 5
- Enregistré le: 17 Nov 2023, 14:54
-
 par Steve17 » 28 Fév 2024, 16:07
par Steve17 » 28 Fév 2024, 16:07
Bonjour Ben (:
Alors
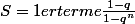
Mais je n'arrive pas à trouver la valeur de x pour laquelle S(x) existe
Modifié en dernier par
Steve17 le 28 Fév 2024, 16:10, modifié 1 fois.
-
Steve17
- Messages: 5
- Enregistré le: 17 Nov 2023, 14:54
-
 par Steve17 » 28 Fév 2024, 16:08
par Steve17 » 28 Fév 2024, 16:08
Je suis un peu perdu (:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 28 Fév 2024, 16:23
par Ben314 » 28 Fév 2024, 16:23
Steve17 a écrit:Alors
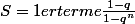
Non, absolument pas.
Et ça me semblerais pas idiot de connaitre le calcul (qu'on peut faire de tête) donnant le résultat vu que ça t'éviterais d'écrire n'importe quoi :
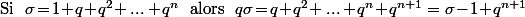
\sigma\!=\!q^{n+1}\!-\!1\ \mbox{ c'est \`a dire }\ \sigma\!=\!\dfrac{1-q^{n+1}}{1-q\ \ }\ \mbox{ si }\ q\!\not=\!1)
Et si on applique ça avec
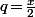
, ça dit que . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Steve17
- Messages: 5
- Enregistré le: 17 Nov 2023, 14:54
-
 par Steve17 » 28 Fév 2024, 18:12
par Steve17 » 28 Fév 2024, 18:12
D'accord je vois... Je me suis un peu embrouillé
Donc pour la question
1)

est une série géométrique de raison
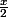
car
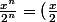^n)
.
Elle converge si

. Donc la série converge pour tout x<2
-
Steve17
- Messages: 5
- Enregistré le: 17 Nov 2023, 14:54
-
 par Steve17 » 28 Fév 2024, 18:46
par Steve17 » 28 Fév 2024, 18:46
Et pour la
2) S=
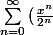}={\sum_{n=0}^{\infty}{(\frac{x}{2}})^n}= \frac{1}{1-\frac{x}{2}})
=

et elle existe lorsque

Donc S(x)=

avec
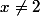

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 28 Fév 2024, 20:36
par Ben314 » 28 Fév 2024, 20:36
Je ne sais pas ce que tu bricole, mais c'est pas mal du grand n'importe quoi :
Déjà,

, ça n'est évidement pas équivalent à
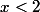
, mais à
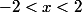
(si

est supposé réel)
Ensuite, il faudrait un minimum de cohérence : tu commence par dire (à tort) qu'il faut que
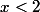
pour que la série converge, puis tu affirme que la série est égal à un truc pour tout
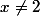
.
Il faudrait se décider : la série elle existe ou elle n'existe pas pour
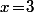
par exemple ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités