Série entière

[Ncdk]

Bonjour,

J'avais une question, je comprends pas pourquoi on fait ce genre de chose, voici l'énoncé :

Je dois trouver le rayon de convergence de la série entière suivante dont le terme général est

Je commence déjà par regarder la suite

Tout d'abord elle ne tend pas vers 0 mais vers

Je voulais savoir pourquoi on continue d'étudier cette série, car ne tend pas vers 0 donc il y a divergence. Le critère de convergence non pas vers 0 mais vers sur ne permet pas de dire que la série entière diverge ?

Je voudrais une petite explication du pourquoi du comment on va dire ça doit être vraiment tout bête mais je voudrais plus être choqué sur ce genre d'exemple

[mathelot]

bonjour,
tu as plusieurs critères de convergence des séries et des séries entières

Cauchy-Hadamard
règle de Riemann
Cauchy
règle de d'Alembert
règle de Raabe et Duhamel

sauf erreur....

à toi de les ordonner logiquement (*)

Avec Cauchy Hadamard

donc sur cet exemple.

(*) méthode de travail
Chaque critère de convergence d'une série est facilement étudiable, pris séparément.
Disons que les démos sont lumineuses.
Une fois que tu as étudié chaque critère de convergence séparément
le travail personnel est de les ordonner logiquement pour
savoir s'ils ont des liens entre eux (implication, équivalence)
et sinon d'exhiber des contre-exemples si non implication.

[Ncdk]

D'accord merci bien :)

[Jouailleur]

C'est une application de la règle de Cauchy qui veut qu'une série diverge ou converge selon la valeur de la limite supérieure du terme ...

La convergence vers 0 n'est pas requise.

Attention, ton calcul de limite est incorrect.

Bonjour,

J'avais une question, je comprends pas pourquoi on fait ce genre de chose, voici l'énoncé :

Je dois trouver le rayon de convergence de la série entière suivante dont le terme général est

Je commence déjà par regarder la suite

Tout d'abord elle ne tend pas vers 0 mais vers

Je voulais savoir pourquoi on continue d'étudier cette série, car ne tend pas vers 0 donc il y a divergence. Le critère de convergence non pas vers 0 mais vers sur ne permet pas de dire que la série entière diverge ?

Je voudrais une petite explication du pourquoi du comment on va dire ça doit être vraiment tout bête mais je voudrais plus être choqué sur ce genre d'exemple

[Ben314]

Je voulais savoir pourquoi on continue d'étudier cette série, car ne tend pas vers 0 donc il y a divergence. Le critère de convergence non pas vers 0 mais vers sur ne permet pas de dire que la série entière diverge ?

Le problème, c'est que... tu mélange tout...
Le fait que la suite ne tende pas vers 0 signifie effectivement que la série est (grossièrement) divergente sauf que la série qu'on te demande d'étudier, ce n'est pas mais .
Si tu regarde bien, le seul truc que ça montre, c'est que, pour z=1, la série entière est (grossièrement) divergente.
Et si tu connait le B-A-BA sur les séries entières, ça te montre que le rayon de C.V. de la série entière est =1.

BILAN : avec un peu de bon sens, le rayon de C.V. de la série est évident et il n'est nulement besoin d'utiliser un quelconque "critère" (on peut si on veut, mais ça fait un peu con dans un cas aussi simple : c'est comme de faire pour résoudre ... )

EDIT : Pour modérer mon propos çi dessus, d'utiliser un "critère", (évidement celui avec la racine n-ième ici), ç'est pas con si tu ne calcule pas la limite des an, mais si tu calcule la limite en question, ça devient très con vu que le résultat devient évident sans aucun "critère".

[mathelot]

il se trouve que



d'autre part donc la convergence (si |z|1) est très rapide,
du coup, dualement, la convergence de peut être très lente.

[Ncdk]

C'est une application de la règle de Cauchy qui veut qu'une série diverge ou converge selon la valeur de la limite supérieure du terme ...

La convergence vers 0 n'est pas requise.

Attention, ton calcul de limite est incorrect.

Je me suis trompé j'ai fait la limite de

Le problème, c'est que... tu mélange tout...
Le fait que la suite ne tende pas vers 0 signifie effectivement que la série est (grossièrement) divergente sauf que la série qu'on te demande d'étudier, ce n'est pas mais .
Si tu regarde bien, le seul truc que ça montre, c'est que, pour z=1, la série entière est (grossièrement) divergente.
Et si tu connait le B-A-BA sur les séries entières, ça te montre que le rayon de C.V. de la série entière est =1.

BILAN : avec un peu de bon sens, le rayon de C.V. de la série est évident et il n'est nulement besoin d'utiliser un quelconque "critère" (on peut si on veut, mais ça fait un peu con dans un cas aussi simple : c'est comme de faire pour résoudre ... )

EDIT : Pour modérer mon propos çi dessus, d'utiliser un "critère", (évidement celui avec la racine n-ième ici), ç'est pas con si tu ne calcule pas la limite des an, mais si tu calcule la limite en question, ça devient très con vu que le résultat devient évident sans aucun "critère".

Je vois bien merci, en fait c'était pour mon assurer que prouver que ne tend pas vers 0 n'influe presque en rien sur ce qu'on cherche.
Mais comme tu en parles, j'ai besoin aussi de m'assurer quelque chose, avec le critère de cauchy on trouve que R=1

Je voulais savoir plusieurs choses, déjà au premier abord on a :

• on a divergence

Si je me trompe pas c'est ça. Il reste maintenant à étudier ce qui se passe sur ce rayon de convergence donc quand .

Mais la ou je suis embêté c'est que z est un complexe et que je peux prendre seulement z = 1 puis étudier donc la série entière où je dois prendre en considération puis donc m'intéresser à

[mathelot]

tu peux considérer


ou


La série a un disque de convergence.Ce disque a un bord , un cercle, disons centré à l'origine , de rayon 1.

tu peux tjrs utiliser la sommation d'Abel si on ne se rapproche pas trop de 1,comme avec les séries alternées.

si il y a de la pathologie, le coup, c'est de considérer des limites radiales,regarde dans Rudin, "complex analysis".

[Ben314]

Je vois bien merci, en fait c'était pour mon assurer que prouver que ne tend pas vers 0 n'influe presque en rien sur ce qu'on cherche.

Ben si, ça influe même fortement vu que ça signifie que pour z=1 la série entière diverge (grossièrement) et donc que le rayon de C.V. est 1[/TEX] on a divergence.[/list][/quote]Oui, et ça, c'est a savoir absolument vu que c'est la définition même du rayon de convergence et qu'en math.,le mini du mini à savoir quand on travaille dans un domaine donné, c'est les définition. Tu peut même rajouter que, dans le cas où |z|>R, la série est grossièrement divergente (donc très façile à repérer : le terme général ne tend pas vers 0) et aussi que, si r<R, la série converge normalement (donc uniformément) sur le disque de centre 0 et de rayon r.
Et je le redit, rien qu'avec ça (donc avec la définition), si on a deux sous de bon sens, ça permet de trouver le rayon de C.V. dans pas mal d'exercices, et en plus, ça a l'intérêt d'obliger à réfléchir un peu plutôt que d'appliquer bourrinement un "critère" donc c'est bien plus formateur.

Si je me trompe pas c'est ça. Il reste maintenant à étudier ce qui se passe sur ce rayon de convergence donc quand

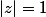
Là, ça dépend de ce que l'énoncé te demande.
S'il te demande uniquement le rayon de C.V., c'est fini (et c'est souvent le seul truc qu'on demande vu que c'est souvent compliqué de voir ce qu'il se passe au bord du disque de convergence)
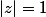
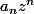
Sauf qu'en fait, ici, c'est super évident : tu as montré que ne tendait pas vers 0 et ça prouve que, si alors ne tend pas vers 0 donc que la série est (grossièrement) divergente : ça ne converge donc nulle part sur le bord du disque.
[et tu te (re)rend compte ici que, contrairement à ce que tu pense, le fait que ne tend pas vers 0 est une information extrêmement utile pour étudier ta série]

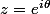
Mais la ou je suis embêté c'est que z est un complexe et que je peux prendre seulement z = 1 puis étudier donc la série entière où je dois prendre en considération puis donc m'intéresser à

Et c'est là que tu voit que pour répondre à cette question, il valait bien mieux avoir précédemment montré que R=1 sans utiliser de "critère" qu'en en utilisant un vu que dans le premier cas, ça donnait immédiatement la réponse.

[Ncdk]

Parfait, merci pour toutes vos explications claires et précises, ça débloque pas mal la façon de raisonner pour d'autres exercices :)

[Ben314]

tu peux tjrs utiliser la sommation d'Abel si on ne se rapproche pas trop de 1...

Par exemple, et sans vouloir être vexant, si mathelot avait calculé le rayon de C.V. sans utiliser de critère, ben il dirait pas ensuite qu'il fallait aller chercher "de la théorie compliquée" (à savoir le critère d'Abel) pour savoir ce qu'il se passe lorsque |z|=1.

Et c'est très exactement pour ça que je t'incite plus que fortement à ne pas y aller totalement "bourrin", c'est à dire à systématiquement utiliser un "critère" pour calculer R (ce qui bien évidement ne veut pas dire non plus qu'il ne faut jamais les utiliser)

[Ncdk]

Si je prends un exemple



J'ai trouvé le Rayon de convergence qui est 1, assez facilement d'ailleurs.

Mais par exemple dans ce cas-là, à part passer par , je ne vois pas comment faire autrement, vu que tend vers 0 quand n va vers l'infini.

[Ben314]

Tu est effectivement là dans le cas "fréquent" où la convergence au bord du disque n'est pas du tout évidente.
Et cette fois, je ne pense pas que tu puisse te passer du critère d'Abel qui va te dire qu'il y a convergence (simple mais pas absolue) pour tout les z tels que |z|=1 SAUF pour z=1.