Série entière

[lapras]

Bonsoir,
je souhaite montrer que le rayon de convergence de cette série entière est R=1 :
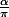
où est irrationel.
Bien sur R <= 1.
Le problème c'est qu'il faut montrer que pour |z|<1, z^n/sin(n*alpha) ne devient pas trop grand.
Or les n*alpha sont dense modulo Pi...
Est ce trivial ? Ou y a t il quand même un peu de travail à faire ?
Lapras

[girdav]

Bonjour,
on peut se servir du fait que si .

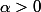
[Doraki]

Il faut montrer que la suite des (;)n) ne conspire pas contre toi en prenant des valeurs trop proches des multiples de ;) trop souvent.
Donc il faut utiliser un argument style le résultat sur les fractions continues qui permet de minorer l'écart entre ;)/;) et un rationnel k/n en fonction de n.

[Actéon]

le stéréotype de l'exercice taupinal... (et pourtant je n'aime pas ce mot...). Je me trompe? :)