Bonjour
Auriez vous des pistes de solutions pour :
"Soit x un réel montrer qu'il existe une série entière de rayon de convergence infini à coeff rationnels qui s'annule en x"
Merci d'avance
Lionel
Série entière qui s'annule en x
10 messages
- Page 1 sur 1
Bonjour
La série ainsi construite, si elle existe est-elle une série entière?
Si x est rationnel, il suffit de prendre une série entière de rayon infini à coefficients rationnels (et il en existe
de rayon infini à coefficients rationnels (et il en existe 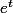 ,
, 
 ) et de considérer la série
) et de considérer la série \sum_0^\infty a_n t^n) qui sera bien une série entière à coefficients rationnels et de rayon infini.
qui sera bien une série entière à coefficients rationnels et de rayon infini.
Si x n'est pas rationnel, je ne vois que la série nulle qui remplit les conditions.
Ben314 a écrit:Salut,
Construire (par récurrence) une suite d'entierstels que, si
on pose
, alors on ait
.
Sauf erreur, il suffit de prendre(partie entière) et tout devrait marcher.
La série ainsi construite, si elle existe est-elle une série entière?
Si x est rationnel, il suffit de prendre une série entière
Si x n'est pas rationnel, je ne vois que la série nulle qui remplit les conditions.
deltab a écrit:Bonjour
La série ainsi construite, si elle existe est-elle une série entière?
Si x est rationnel, il suffit de prendre une série entièrede rayon infini à coefficients rationnels (et il en existe
,

) et de considérer la série
qui sera bien une série entière à coefficients rationnels et de rayon infini.
Si x n'est pas rationnel, je ne vois que la série nulle qui remplit les conditions.
Pour x rationnel pourquoi faire compliqué, il suffit de prendre la série -x+t = -x + t + 0*t² + 0*t^3 + ...
L'exercice n'a d'intérêt que pour x non rationnel.
Bonsoir.
Il y a alors un petit problème de notations. si par série tu entends , comme tu l'as fait pour S_n, tu as construit une série numérique et non une série entière à moins de considérer S_n(t)=... et la série
, comme tu l'as fait pour S_n, tu as construit une série numérique et non une série entière à moins de considérer S_n(t)=... et la série }{n!}t^n)
mrif a écrit:Pour x rationnel pourquoi faire compliqué, il suffit de prendre la série -x+t = -x + t + 0*t² + 0*t^3 + ...
L'exercice n'a d'intérêt que pour x non rationnel.
Il y a alors un petit problème de notations. si par série tu entends
deltab a écrit:Bonsoir.
Il y a alors un petit problème de notations. si par série tu entends, comme tu l'as fait pour S_n, tu as construit une série numérique et non une série entière à moins de considérer S_n(t)=... et la série
Je n'ai pas de solution au problème et je n'ai pas compris la solution proposée par ben314.
Mais ce qui est sûr c'est que dans le cas où x est rationnel, il n'y a rien à faire puisque tout polynome est une série entière de rayon de convergence infini, et en particulier le polynome P défini par P(X) = X-x est une série entière qui convient.
Bonjour
Toutes mes excuses, je t'avais attribué la construction proposée par ben314.
Les solutions, il y a au moins une la série nulle déjà proposée.
Mais à quoi bon se casser la tête, lionel52 est l'auteur du topic, il est déjà parti en vacances ou il est en train de rire (ou les deux)
mrif a écrit:Je n'ai pas de solution au problème et je n'ai pas compris la solution proposée par ben314.
Mais ce qui est sûr c'est que dans le cas où x est rationnel, il n'y a rien à faire puisque tout polynome est une série entière de rayon de convergence infini, et en particulier le polynome P défini par P(X) = X-x est une série entière qui convient.
Toutes mes excuses, je t'avais attribué la construction proposée par ben314.
Les solutions, il y a au moins une la série nulle déjà proposée.
Monsieur23 a écrit:Aloha,
Pour troller, je dirais bien que la fonction nulle convient
Mais à quoi bon se casser la tête, lionel52 est l'auteur du topic, il est déjà parti en vacances ou il est en train de rire (ou les deux)
Mon truc n'est effectivement peut-être pas trés clair.deltab a écrit:Il y a alors un petit problème de notations. si par série tu entends, comme tu l'as fait pour S_n, tu as construit une série numérique et non une série entière à moins de considérer S_n(t)=... et la série
Pour construire les
Aprés, une fois tout les
Vu la construction des
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
