Bonsoir.
On se donne

entiers
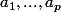
strictement positifs et distincts et un polynôme

de degré strictement plus petit que

.
On se propose de calculer la somme de la série entière qui a pour terme général:
x^n}{\prod_{j=1}^p{(n+a_j)}})
.
Voici ce que j'ai fait.
On considère la fraction rationnelle
}{\prod_{j=1}^p{(n+a_j)}})
. D'après l'hypothèse faite sur

, on peut directement faire la décomposition en éléments simples (pas de division euclidienne).
On a donc:
}{\prod_{j=1}^p{(n+a_j)}} = \ \sum_{j=1}^p{\frac{A_i}{(n+a_j)}})
On trouve
}{\prod_{\overset{j=1}{j \neq k}}^p{(aj-a_k)}})
Tout se ramène donc à regarder la somme des

séries entières
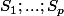
, où le terme général de la série
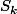
est
x^n}{\prod_{\overset{j=1}{j \neq k}}^p{(aj-a_k)}(n+a_k)})
.
On doit alors calculer
 = \sum_{n=0}^{+\infty}{\frac{x^n}{(n+a_j)}})
On pose
 = \sum_{n=0}^{+\infty}{\frac{x^{n+a_k}}{(n+a_j)}})
On a
 = \sum_{n=0}^{+\infty}{x^{n+a_k-1}})
soit
 =\frac{x^{a_k-1}}{1-x} = -\frac{x^{a_k-1}}{x-1}= -\left\(\frac{x^{a_k-1} -1 +1}{x-1} \right\))
et là soit
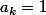
auquel cas
=- \ln (1-x))
soit
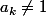
et dans ce cas
 = -\sum_{j=0}^{a_k-2}{x^j}- \frac{1}{1-x})
et en intégrant
 = -\sum_{j=0}^{a_k-2}{\left\(\frac{x^{j+1}}{j+1}\right\)} + \ln (1-x))
d'où
 = \frac{h(x)}{x^{a_k}})
pour x non nul,
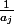
pour

. On a alors que pour x non nul
 = \frac{-\sum_{j=0}^{a_k-2}{\left\(\frac{x^{j+1}}{j+1}\right\)} + \ln (1-x) }{x^{a_k}} = <br />\frac{-\sum_{j=1}^{a_k-1}{\left\(\frac{x^{j}}{j}\right\)} + \ln (1-x) }{x^{a_k}})
donc
\left\( \ln (1-x)-\sum_{j=1}^{a_k-1}{\left\(\frac{x^{j}}{j}\right\)}\right\) }{\prod_{\overset{j=1}{j \neq k}}^p{(aj-a_k)}x^{a_k}})
On somme ensuite tout cela sur

On a:
x^n}{\prod_{j=1}^p{(n+a_j)}}} =\ \sum_{k=1}^p{\frac{P(-a_k)\left\( \ln (1-x)-\sum_{j=1}^{a_k-1}{\left\(\frac{x^{j}}{j}\right\)}\right\) }{\prod_{\overset{j=1}{j \neq k}}^p{(aj-a_k)}x^{a_k}}}<br />= \ln(1-x).\sum_{k=1}^p{\frac{P(-a_k)}{\prod_{\overset{j=1}{j \neq k}}^p{(aj-a_k)}x^{a_k}}}- \sum_{k=1}^p{\frac{P(-a_k)}{\prod_{\overset{j=1}{j \neq k}}^p{(aj-a_k)}x^{a_k}}}\sum_{j=1}^{a_k-1}{\frac{x^j}{j}})
C'est là qu'il faut utiliser l'hypothèse selon laquelle les

sont distincts: on a, quitte à réindicer les

, que
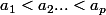
On regarde d'abord le cas
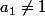
Alors dans la somme du deuxième terme, les termes en
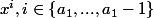
apparaissent p fois, les termes en
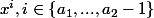
apparaissent

fois etc...
Si
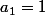
on commence à partir de
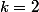
mais la remarque précédente est plus pénible à mettre en forme.
Le cas

se traite à partir de l'écriture initiale de la série.
J'ai oublié de préciser que le rayon de convergence de la série étudiée est 1.
Y a-t-il une méthode plus rapide pour arriver au résultat?
Et ce que j'ai fait est correct ou non?
Dans tous les cas félicitations de m'avoir lu jusqu'au bout!
