Sequence exacte

[arsene]

Bonsoir.
Je resouds un probleme d algebre sur les sequences ou suites exactes.
Je veux trouver deux exemples de A tels que la suite suivante soit exacte
0 ---> Z----> A---> Z/2Z ---> 0
j ai trouvé le 1er exemple et demontre bien que c'est exact.J'espere que dans mes demarches je n ai fait aucune betise.
J ai pris A=2Z et l application f ki a chak nbre retourne son double.
Avez vous une objektion?
Et pour un deuxieme exemple pourriez vous me donnez une idee?
Merci

[Nightmare]

Salut :happy3:

Si je comprends bien, tu gardes le même morphisme pour ta suite. Ce dernier n'envoie pas 2Z sur Z/2Z !

[skilveg]

Ton application est bien celle de gauche? Auquel cas ça ne marche pas, c'est une bijection entre et ... En revanche si le terme du milieu est ça fonctionne.

Pour avoir d'autres exemples, tu pourrais regarder des termes centraux du genre .

[arsene]

Salut :happy3:

Si je comprends bien, tu gardes le même morphisme pour ta suite. Ce dernier n'envoie pas 2Z sur Z/2Z !

le premier morphisme est de Z vers 2Z a chak elt renvoie son double
le deuxieme je veux le definir de 2Z vers Z/2Z ki a chak elt associe son reste dans la division par deux.(je ne comprends pas tres bien les classes dequivalence mais bon...)

[arsene]

Ton application est bien celle de gauche? Auquel cas ça ne marche pas, c'est une bijection entre et ... En revanche si le terme du milieu est ça fonctionne pas

oui
kelle soit une injektion m arrange.Si elle est bijective pourkoi ca pose probleme.Ca ne va rien diminuer a mon avis aux caracteristiques que doivent avoir mon application.
ou alors je ne pige pas bien la notion :triste:

[skilveg]

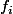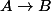C'est quoi pour toi une suite exacte? Pour moi, c'est une suite d'objets (groupes par exemple) et des morphismes tels que l'image de soit le noyau de . En particulier, est exacte si est injective, 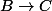surjective et si l'image de la première est le noyau de la seconde.

Si tu écris la suite , elle ne peut pas être exacte: la flèche devrait être surjective et de noyau 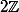, ce qui est impossible.

En revanche, la suite est bien exacte, c'est ça que je voulais dire.

[Doraki]

Tu n'as pas précisé quel était ton morphisme de 2Z dans Z/2Z.

Ah si, t'as choisi le morphisme x -> 0.
Et il est pas surjectif donc la partie 2Z -> Z/2Z -> 0 n'est pas exacte.

[arsene]

Pour avoir d'autres exemples, tu pourrais regarder des termes centraux du genre .

En fait l image de l application de gauche doit etre egale au noyau de celle de droite.
Bon de cette maniere je ne me retrouve pas
0 --> Z --> Z*Z --> 2Z --> 0
0 , e , (e,e) , ê 0
Im de gauche est Z et ker droite est 2Z
La suite nest pas exacte.
Si je mets 2Z*2Z le probleme est il resolu?

[arsene]

Ah si, t'as choisi le morphisme x -> 0.
Et il est pas surjectif donc la partie 2Z -> Z/2Z -> 0 n'est pas exacte.

c est vrai

[skilveg]

Pour un autre exemple je pensais à
[CENTER][/CENTER]

[arsene]

UNE QUESTION QUI ME VIENT A LESPRIT COMME CA
l ensemble Z*nZ est il isomorphe a nZ*Z?

[Nightmare]

D'après toi?

[arsene]

D'après toi?

d apres moi ils sont isomorphes.nZ est isomorphe a Z car si je ne me trompe pas une fois de plus.donc d ou l isomorphie des deux.la 1ere composante est isomorphe a la deucieme et la seconde aussi a la seconde composante.
mais avec les produits de groupe je me demande si c sans faute ce que je dis

[arsene]

merci pour vos explications

[Nightmare]

d apres moi ils sont isomorphes.nZ est isomorphe a Z car si je ne me trompe pas une fois de plus.donc d ou l isomorphie des deux.la 1ere composante est isomorphe a la deucieme et la seconde aussi a la seconde composante.
mais avec les produits de groupe je me demande si c sans faute ce que je dis

Bien sûr, on prend l'application de ZxnZ dans nZxZ qui à (x,y) associe (y,x) ! C'est clairement un isomorphisme :happy3: