La Riemann-intégrabilité

[eratos]

salut! je suis à fond dans les intégrales aujourd'hui ...
on a une fonction bizarroïde:
f:[0,1]->R
f(x)=0 si x=0 ou x irrationnel
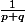
f(x)= si x=p/q, (fraction irréductible)

Il faut montrer qu'elle est intégrable (au sens de Riemann, lebesgue c'est loin devant)... ça m'intrigue parce que, elle n'a l'air nulle part continue. Je savais qu'il y avait des fonctions continues partout dérivable nulle part. Ce serait un truc de ce goût là?

En fait, quelque soit un réel positif(epsilon) faut trouver deux fonctions en escalier pour encadrer f, et que l'intégrale de leur différence soit inférieur à epsilon?

pour minorer f, brutalement la fonction nulle fonctionne, mais alors pour la majorer :mur:

[Doraki]

Ouais il faut montrer qu'en faisant des subdivisions suffisemment petites, tu obtiens des fonctions en escalier plus gandes que f dont les intégrales tendent vers 0.

Il faut commencer par remarquer que pour tout ;)>0, il n'y a qu'un nombre fini de valeurs de x pour lesquelles f(x) > ;), et donc que si tu fais des subdivisions suffisemment petites, la graaande majorité de tes rectangle vont être de hauteur plus petite que ;), donc tu pourras sûrement trouver une fonction en escalier qui majore f et dont l'intégrale est <= 2;).

[Nightmare]

Hello,

c'est pas possible que la fonction soit discontinue partout, elle ne serait pas intégrable.

Elle est continue sur les irrationnels :

Si Rn=(pn)/(qn) est une suite de rationnels irréductibles tendant vers x irrationnel, alors c'est pas trop dur de voir que nécessairement pn et qn tendent vers +oo et donc que f(Rn)=1/(pn+qn) tend vers 0=f(x). On a bien continuité en x.

Les points de discontinuités sont dénombrables, donc la fonction est bien Riemann-intégrable.

[eratos]

Hello,

c'est pas possible que la fonction soit discontinue partout, elle ne serait pas intégrable.

Elle est continue sur les irrationnels :

Si Rn=(pn)/(qn) est une suite de rationnels irréductibles tendant vers x irrationnel, alors c'est pas trop dur de voir que nécessairement pn et qn tendent vers +oo et donc que f(Rn)=1/(pn+qn) tend vers 0=f(x). On a bien continuité en x.

Les points de discontinuités sont dénombrables, donc la fonction est bien Riemann-intégrable.

Un grand soulagement, je me suis fais peur, merci beaucoup. :lol3:

g0, il existe un rang N tel que n>N =><epsilon.

Mais je me rend compte que ça va pas...

[Doraki]

une subdivision du style .

où est-ce que tu es allé chercher une idée aussi saugrenue ?
là t'es en train de subdiviser [1/n ; l'infini[ en n morceaux. Ce qui n'est pas du tout une subdivision de [0;1]

En général on prend, pour un entier n, la subdivision en n segments de longueur 1/n : [0;1/n] ; [1/n;2/n] ... [(n-1)/n ; n/n = 1].

[eratos]

où est-ce que tu es allé chercher une idée aussi saugrenue ?
là t'es en train de subdiviser [1/n ; l'infini[ en n morceaux. Ce qui n'est pas du tout une subdivision de [0;1]

En général on prend, pour un entier n, la subdivision en n segments de longueur 1/n : [0;1/n] ; [1/n;2/n] ... [(n-1)/n ; n/n = 1].

Bah c'est exactement à ça que je pensais :girl2: