Revision Prepa ECE

[vannou]

Coucou les gens ! Je suis nouvelle ici, bon du coup je me lance car j'aurais besoin de votre aide pour un exo dont je ne comprends pas le sens (est-ce parce que c'est le debut des vacances, ou que je ne connais pas mon cours... allez savoir! :) ) Donc je vous l'envoie, pis si vous pouviez me donner quelques pistes pour chaque question et developper vous seriez top =)

Partie 1

On pose, pour tout entier n superieur ou egale a 1: Vn = Somme de k=1 à n de 1/k
1) Montrer que pour tout k de N*, 1/(k+1) est inferieur ou égale à l'intégrale de k a k+1 de 1/t.dt
2) En deduire que pour tout n de N*, vn est inferieur ou egale à ln(n)+1

On considere la suite (Un) définie par son premier terme Uo=1 et par la relation suivante, valable pour tout n de N: U(n+1)= Un +1/Un
1) a. Montrer par récurrence que chaque terme de cette suite est parfaitement défini et strictement positif
b. En déduire le sens de variation de la suite (un)
2) a. Pour k de N, exprimer U^2(k+1) - U^2(k) en fonction de U^2(k)
b. En déduire que pour tout n dans N*, U^2(n)= 2n + 1 + Somme de k=0 a n-1 de 1/(U^2(k))
c. Montrer que pour tout n de N*, (Un)^2 supérieur ou égale a 2n + 1. En déduire la limite de la suite (un)

Bon il a le reste mais si déjà je fais çà c'est pas mal, sa m'avancera pour comprendre le reste =)
Voila donc merci aux courageux qui prendront la peine de m'aider

[mathelot]

Bonjour,

pour la (1),il s'agit de sommes de Darboux de l'intégrale
la fonction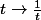 est décroissante sur [k;k+1]
donc minorée par la fonction constante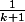
après on intègre en utilisant Chasles


pour la (2)
le truc est d'élever au carré, ce qui fait apparaitre le double produit 2ab=2
On en déduit que en minorant.

ton devoir porte essentiellement sur la relation d'ordre >