Résultats de Sylow
16 messages
- Page 1 sur 1
résultats de Sylow
Bonjour, j'essaie de démontrer les résultats de Sylow mais je coince à quelques endroits...
HYPOTHESES
On considère un nombre premier p, et un groupe G d'ordre m.p^n où m est premier à p.
Soit Z le centre de G .
TOUT DEBUT DE LA DEMONSTRATION
Si Z est divisible par p alors Z contient un sous-groupe cyclique d'ordre p, appelons le D.
Je sais que si D est un sous-groupe de Z alors l'ordre de D divise l'ordre de Z. Mais en quoi cette "réciproque" est vraie? C'est un résultat général ou le fait que Z soit le centre de G y est pour quelque chose? On pourrait me la démontrer rapidement svp??
HYPOTHESES
On considère un nombre premier p, et un groupe G d'ordre m.p^n où m est premier à p.
Soit Z le centre de G .
TOUT DEBUT DE LA DEMONSTRATION
Si Z est divisible par p alors Z contient un sous-groupe cyclique d'ordre p, appelons le D.
Je sais que si D est un sous-groupe de Z alors l'ordre de D divise l'ordre de Z. Mais en quoi cette "réciproque" est vraie? C'est un résultat général ou le fait que Z soit le centre de G y est pour quelque chose? On pourrait me la démontrer rapidement svp??
Je suppose que tu veux dire « si l'ordre de Z est divisible par p... »
Ca vient d'un résultat sur les groupes abéliens finis : Si G est un groupe abélien fini et p divise le cardinal de G (p premier), alors il existe un élément de G d'ordre p.
Si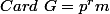 , p ne divisant pas m, on peut faire une démonstration par récurrence (forte) sur m (à r fixé).
, p ne divisant pas m, on peut faire une démonstration par récurrence (forte) sur m (à r fixé).
Si m = 1, soit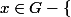 , l'ordre de
, l'ordre de  est égal à
est égal à 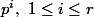 , et
, et 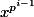 est d'ordre
est d'ordre  .
.
Si le résultat est vrai pour tout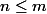 , soit
, soit 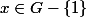 .
.
- si p divise l'ordre de x (noté [x]), est un élément d'ordre p de G.
est un élément d'ordre p de G.
- si p ne divise pas l'ordre de x, soit H le sous-groupe de G engendré par x. Comme G est abélien, H est distingué dans G, et G/H est un groupe abélien de cardinal , par hypothèse de récurrence il existe un élément d'ordre p dans G/H, autrement dit il existe un élément
, par hypothèse de récurrence il existe un élément d'ordre p dans G/H, autrement dit il existe un élément 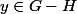 tel que
tel que 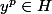 , donc par le théorème de Lagrange,
, donc par le théorème de Lagrange, ^{\[x\]} = (y^{\[x\]})^p = 1) . De plus
. De plus  , car si c'était le cas, on aurait
, car si c'était le cas, on aurait  et
et 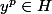 , et comme p et [x] sont premiers entre eux, par Bezout on obtiendrait
, et comme p et [x] sont premiers entre eux, par Bezout on obtiendrait  . On a dont trouvé un élément d'ordre p de G.
. On a dont trouvé un élément d'ordre p de G.
Ca vient d'un résultat sur les groupes abéliens finis : Si G est un groupe abélien fini et p divise le cardinal de G (p premier), alors il existe un élément de G d'ordre p.
Si
Si m = 1, soit
Si le résultat est vrai pour tout
- si p divise l'ordre de x (noté [x]),
- si p ne divise pas l'ordre de x, soit H le sous-groupe de G engendré par x. Comme G est abélien, H est distingué dans G, et G/H est un groupe abélien de cardinal
Je n'ai également pas compris le point suivant:
Voila ce que j'ai compris:
il existe un élément d'ordre p dans G/H, autrement dit un sous-groupe de G cyclique (car p premier) d'ordre p, donc il existe un y dans G-H d'ordre p qui engendre ce sous-groupe cyclique [jusque là c'est bon?].
abcd22 a écrit:...il existe un élément d'ordre p dans G/H, autrement dit il existe un élémenttel que
, donc par le théorème de Lagrange,
.
Voila ce que j'ai compris:
il existe un élément d'ordre p dans G/H, autrement dit un sous-groupe de G cyclique (car p premier) d'ordre p, donc il existe un y dans G-H d'ordre p qui engendre ce sous-groupe cyclique [jusque là c'est bon?].
abcd22 a écrit:G/H est un groupe abélien de cardinal
Les éléments de G/H sont des sous-ensembles de G, je ne comprends pas le terme "abélien " ici, qu'est-ce qui commutent?? les sous-ensembles?
abcd22 a écrit:il existe un élément d'ordre p dans G/H, autrement dit il existe un élémenttel que
A peu près la même question. un sous-ensemble d'ordre p?
ce serait plutot un sous-groupe d'ordre p, mais les élements de G/H ne sont pas des sous-groupes de G (hormis H).
merci
En fait je fais une récurrence sur m, avec 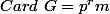 , on suppose le résultat vrai pour les groupes abéliens H tels que
, on suppose le résultat vrai pour les groupes abéliens H tels que 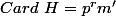 avec m'<m, comme le cardinal de
avec m'<m, comme le cardinal de 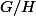 est
est  ,
, 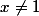 donc
donc  , on peut appliquer l'hypothèse de récurrence à G/H.
, on peut appliquer l'hypothèse de récurrence à G/H.
On pourrait aussi dire qu'on fait la récurrence sur le cardinal de G, avec l'hypothèse que p divise le cardinal du groupe, ça revient au même, j'ai dit que je faisais la récurrence sur m parce que la puissance de p dans le cardinal du quotient est la même que dans le cardinal de G.
On pourrait aussi dire qu'on fait la récurrence sur le cardinal de G, avec l'hypothèse que p divise le cardinal du groupe, ça revient au même, j'ai dit que je faisais la récurrence sur m parce que la puissance de p dans le cardinal du quotient est la même que dans le cardinal de G.
abcd22 a écrit:par le théorème de Lagrange,.
je ne vois pas le rapport entre le théorème de Lagrange (l'ordre d'un sous-groupe divise l'ordre du groupe en question) et le fait que (a^p)^q=(a^q)^p qui est tout le temps vrai non???
_______________________________
Et aussi, je n'arrive pas à démontrer que si
simplet a écrit:Et ce n'est pas parce que la classe de y était d'ordre p que y l'est aussi!! (par hasard il n'y aurait pas un petit résultat qui controlerait ca??
On peut dire que si la classe de y est d'ordre p dans G/H et que H est de cardinal n, l'ordre de y dans G divise
désolé d'avoir monopolisé ta journée
merci beaucoup
de rien !
[#] On peut même prendre tout le cercle unité de
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
