Salut à tous. En résolvant un exercice, je me suis aperçu que j'avais en fait démontré en fait un autre résultat et je voulais m'assurer que tout ceci était correct.
Soit F et G deux espaces métriques complets. Montrer que FUG est complet.
En montrant ceci, j'ai aussi montré que si F et G sont complets, alors l'intersection F inter G est non vide!
Soit
_n)
une suite de Cauchy de
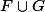
.
Soit

une application de N -> N définie par :
 = min(n >0,x_n \in F))
 = min( n>\phi(0), x_n \in F))
et par récurrence on définit :
 = min( n>\phi(n), x_n \in F))
Tous ces "min" existent bien car on a à faire à des parties de N.
Ainsi, la suite
}))
est une suite extraite de
_n)
et est une suite de

. Comme une sous suite d'une suite de Cauchy reste une suite de Cauchy, on peut affirmer que
}))
est une suite de Cauchy de F donc elle converge vers une limite l dans F (donc dans FUG) car F est complet.
Ainsi, la suite
_n)
est une suite de Cauchy de FUG qui admet un point adhérent

dans FUG donc elle converge vers

donc FUG est complet.
Voilà. A partir de là, on pourrait faire le même raisonnement avec G plutôt que F et on conclurait que
_n)
converge vers

. Par unicité de la limite, on aurait l = l' donc l est un élément de F inter G donc F inter G est non vide.
Ce résultat est-il correct ?
Mais il doit y avoir une erreur car par exemple le segment [-1,1] est complet, de même pour [2,3] alors que l'intersection est vide..
Merci d'avane.
