Bonjour à tous,
J'ai grand besoin d'aide. Je suis géographe de formation et en matière de mathématique, même si j'ai bien progressé depuis le lycée, je suis resté tout de même partiellement sur mes acquis.
Alors voila, j'ai besoin d'exprimer Vi en fonction de gi. Comment faire, avec une méthode simple, dans cette expression car la je sèche, il me manque probablement des connaissances (J'avais bien pensé partir avec une dérivation qc) ?
Vi = Vmin*exp(-(1/a)*(Ggi/Vi)^a).
Merci de votre aide à tous.
Resoudre une équation avec x et exp(x^a)
5 messages
- Page 1 sur 1
Bonjour,
j'ai réécrit ton équation en termes plus mathématiques
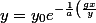^a})
il est impossible d'obtenir une formule close donnant fonction explicite de
fonction explicite de 
néammoins, il y a un théorème pour ce genre de situation:
"théorème des fonctions implicites" qui permet d'avoir une formules "locale"
ie, valide dans un petit voisinage de , et l'on calcule les dérivées successives
, et l'on calcule les dérivées successives
de y , relativement à la variable x
j'ai réécrit ton équation en termes plus mathématiques
il est impossible d'obtenir une formule close donnant
néammoins, il y a un théorème pour ce genre de situation:
"théorème des fonctions implicites" qui permet d'avoir une formules "locale"
ie, valide dans un petit voisinage de
de y , relativement à la variable x
Bonjour,
Il est possible d'exprimer explicitement la (ou les) solution(s) de cette équation. Mais cela ne peut pas se faire avec un nombre fini de fonctions élémentaires. Il faut faire appel à une fonction peu connue, la fonction W(X) de Lambert :
Vi = x/(-W(X))^(1/a) avec X =a/((Vmin/k)^a) et k = (-(1/a)(gx)^a)^(1/a)
Ceci requiert de posséder un logiciel de calcul dans lequel cette fonction W de Lambert est implémentée (de la même façon que l'on utilise les fonctions sin(X), ou ln(X), ou etc...).
En pratique, on ne procède pas de cette façon. En effet, il est plus simple de résoudre l'équation par une quelconque méthode de calcul numérique : Newton-Raphson par exemple, ou beaucoup d'autres.
Il est possible d'exprimer explicitement la (ou les) solution(s) de cette équation. Mais cela ne peut pas se faire avec un nombre fini de fonctions élémentaires. Il faut faire appel à une fonction peu connue, la fonction W(X) de Lambert :
Vi = x/(-W(X))^(1/a) avec X =a/((Vmin/k)^a) et k = (-(1/a)(gx)^a)^(1/a)
Ceci requiert de posséder un logiciel de calcul dans lequel cette fonction W de Lambert est implémentée (de la même façon que l'on utilise les fonctions sin(X), ou ln(X), ou etc...).
En pratique, on ne procède pas de cette façon. En effet, il est plus simple de résoudre l'équation par une quelconque méthode de calcul numérique : Newton-Raphson par exemple, ou beaucoup d'autres.
lire ici...................................
dans le domaine réel,
=xe^{x}) , a de bonnes propriétés sur R+ (continuité, croissance stricte,ressemblance avec une exponentielle) et l'idée est de travailler avec sa (une de ses ) fonction réciproque(s)
, a de bonnes propriétés sur R+ (continuité, croissance stricte,ressemblance avec une exponentielle) et l'idée est de travailler avec sa (une de ses ) fonction réciproque(s) 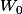
dans le domaine réel,
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
