Résoudre un système
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 06 Aoû 2006, 13:33
par nada-top » 06 Aoû 2006, 13:33
bonjour
voilà un autre probleme ou je bloque j'espère trouver des réponses ici ...
résoudre dans
)
le système suivant :
 : \left\{<br /> \begin{array}{ll}<br /> A \cup X = B \\<br /> <br /> A \cap X = C \\<br /> \end{array}<br /> \right.)
[FONT=Comic Sans MS]
tel que[/FONT]

c'est clair que
 : \left\{<br /> \begin{array}{ll}<br /> X \subseteq \bar{A} \cup C\\<br /> <br /> X \subseteq B \\<br /> \end{array}<br /> \right.)
mais je sais pas comment exprimer l'ensembles des solutions (si j'ai fini biensur) :triste:
pas de solutions directes svp justes des indices. :we:
-
buzard
- Membre Relatif
- Messages: 274
- Enregistré le: 22 Mai 2006, 14:29
-
 par buzard » 06 Aoû 2006, 15:23
par buzard » 06 Aoû 2006, 15:23
Je ne pense pas qu'on puisse parler d'ensemble de solution, car tes équations sont des égalités. Ne serais-ce que la première, elle ne possède qu'une seule solution, il suffit de vérifier qu'elle colle avec la seconde.
Pour la notation, comme d'habitude. Soit il y a une solution et alors tu la donne tel qu'elle, soit il n'y en a pas et l'affaire est réglé à la base.
Sinon tu peut toujours parler de l'ensemble des solutions :
S =

ou S = {F}, si F est la solution au système.
-
Chimomo
- Membre Relatif
- Messages: 275
- Enregistré le: 17 Juin 2006, 09:23
-
 par Chimomo » 06 Aoû 2006, 19:22
par Chimomo » 06 Aoû 2006, 19:22
Attention, l'équation 1 n'a pas qu'une seule solution, ce sont des équations ensembliste.
Par exemple X = (B privé de A) est une solution de l'équation 1 mais X = B est aussi une solution.
Il y a donc bien un ensemble de solutions.
-
Chimomo
- Membre Relatif
- Messages: 275
- Enregistré le: 17 Juin 2006, 09:23
-
 par Chimomo » 06 Aoû 2006, 19:25
par Chimomo » 06 Aoû 2006, 19:25
L'ensemble des oslutions tu l'as, il est de la forme {X inclus dans P(E) tels que G inclus dans X inclus dans H} avec deux ensembles G et H à préciser.
Je te laisse finir.
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 06 Aoû 2006, 19:58
par alben » 06 Aoû 2006, 19:58
Chimomo a écrit: Il y a donc bien un ensemble de solutions.
Bonjour,
Je ne comprends pas ce que signifie le 1 de l'équation 1.
A, B et C étant donnés, il n'y a bien qu'une seule solution au système.
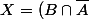\cup C)
.
Ce qui est moins simple c'est de "démontrer" l'égalité.
On peut essayer de la déduire des équations par un raisonnement purement algébrique.
-
Chimomo
- Membre Relatif
- Messages: 275
- Enregistré le: 17 Juin 2006, 09:23
-
 par Chimomo » 06 Aoû 2006, 20:47
par Chimomo » 06 Aoû 2006, 20:47
Je récidive : l'équation (A union X) = B a plusieurs solutions, j'en donne deux pour preuve : B est solution évidente, mais si B est différent de A, B\A est aussi solution. De façon générale, tout ensemble inclus dans B et contenant B\A est solution.
L'ensemble des solutions est donc {

}.
On peut de même trouver l'ensemble des solutions de l'équation (A inter X) = B et il n'y en a pas qu'une seule.
Je ne sait pas pourquoi vous ne voulez pas me croire, mais une équation ensembliste est loin de n'avoir qu'une solution, même quand on a un système de deux équations. Nada-Top a très bien résolu son système.
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 07 Aoû 2006, 00:03
par nada-top » 07 Aoû 2006, 00:03
Hola
Je récidive : l'équation (A union X) = B a plusieurs solutions, j'en donne deux pour preuve : B est solution évidente, mais si B est différent de A, B\A est aussi solution. De façon générale, tout ensemble inclus dans B et contenant B\A est solution.
L'ensemble des solutions est donc {

}.
On peut de même trouver l'ensemble des solutions de l'équation (A inter X) = B et il n'y en a pas qu'une seule.
Chimomo a parfaitement raison ..j'ai essayé de résoudre l'équation
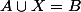
et ça donne la meme chose ..
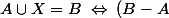 \cap (A \cup X ) \;=\; (B - A) \cap B)
 \cap A ] \cup [ (B-A) \cap X ] = B-A \;)
 \cap X ] \;=\; B - A)
 \subseteq X \;<br />\Leftrightarrow\; (B - A ) \subseteq X \subseteq B \;)

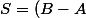 \subseteq X \subseteq B : X \in \mathfrak{P}(E) } ))
je continue demain :dodo: :dodo:
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 07 Aoû 2006, 04:44
par alben » 07 Aoû 2006, 04:44
Bonjour,
Je pense que l'on ne s'est pas bien compris : il s'agit d'un
système de deux équations. Chacune d'entre elles, prise individuellement donne une famille de solutions mais une seule satisfait aux deux équations.
Exemple de démonstration algébrique
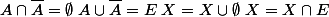
Donc
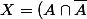\cup [X \cap (A \cup \bar{A})])
En utilisant la distributivité de l' inter, on trouve
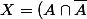\cup [(X \cap A)\cup(X \cap \bar{A})]=[A \cap \bar{A})\cup(X \cap \bar{A})]\cup C)
Puis encore
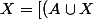 \cap \bar{A}]\cup C=(B \cap \bar{A})\cup C)
On aboutit bien à une solution unique par une méthode comparable aux exos d'algèbre.
Il y a sans doute plus élégant...
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 07 Aoû 2006, 10:46
par nada-top » 07 Aoû 2006, 10:46
bonjour ...
donc on est bien d'accord que la première équation a plusieurs solutions et je vois aussi que l'ensemble des solutions peut s'écrire aussi de cett forme
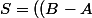 \cup Y \;\; Y \in \mathfrak{P}(A) ))
donc l'équation a plusieurs solutions mais j'ai démontré aussi en résolvant le système que
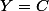
:hein: , donc je crois que alben a raison
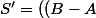 \cup C ))
comme solution du système non?
j'ai remarqué ça dés que j'ai obtenu

mais j'étais pas sure :triste: car je sais seulement comment résoudre des petites équations ensemblistes et ça me donne tj un ensemble solutions pour les systemes je sais pas ...
c'est ça ou je me trompe ? mettez vous d'accord , je suis un peu perdu :doh:
-
Chimomo
- Membre Relatif
- Messages: 275
- Enregistré le: 17 Juin 2006, 09:23
-
 par Chimomo » 07 Aoû 2006, 10:47
par Chimomo » 07 Aoû 2006, 10:47
Désolé mais comme avant Buzard avait dit que chaque équation n'avait qu'une solution...
Cependant, même si ce que tu as fait me parait incontestable, il semblerait logique que la solution du système soit l'intersection des ensembles de solutions des deux équations. Reste à justifier que cette intersection est bien réduite au seul élément que tu donnes.
Je tiens aussi à ajouter que dans des conditions différentes de tels systèmes peuvent ne pas avoir qu'une solution (si les deux équations portent sur des réunions par exemple).
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 07 Aoû 2006, 13:47
par nada-top » 07 Aoû 2006, 13:47
posté par chimomo
Reste à justifier que cette intersection est bien réduite au seul élément que tu donnes.
tu veux dire ça :
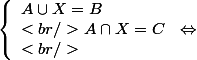
\cup Y \\<br /> A \cap [(B-A) \cup Y ] = C \\<br /> \end{array}<br /> \right.\Leftrightarrow\;)
\cup Y \\<br /> [A \cap (B-A)] \cup (Y\cap A) = C \\<br /> \end{array}<br /> \right.)
et puisque
] = \emptyset \;et\; Y\cap A = Y)
donc
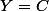
D'ou on conclut ...
merci à vous tous :we:
-
Chimomo
- Membre Relatif
- Messages: 275
- Enregistré le: 17 Juin 2006, 09:23
-
 par Chimomo » 07 Aoû 2006, 13:59
par Chimomo » 07 Aoû 2006, 13:59
Ce n'es pas tout à fait ce que je voulais dire (mais c'est une reformulation de la démo de alben) mais de toute façon le problème étant résolu, ça n'a aucune importance.
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 07 Aoû 2006, 14:08
par nada-top » 07 Aoû 2006, 14:08
ok merci encore :++:
au prochain exo :we:
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 08 Aoû 2006, 08:41
par alben » 08 Aoû 2006, 08:41
Bonjour,
Juste pour conclure, on peut effectivement raisonner par familles de solutions
L'équation 1 équivaut à

L'équation 2 équivaut à

Il reste à marier ces deux inégalités, pour cela il faut savoir que
Appliqué à nos inégalités cela donne :
 \cup C \subset X \subset B \cap (C \cup \bar{A})=(B \cap C) \cup \(B \cap \bar{A})=C \cup \(B \cap \bar{A})\; car \;C \subset B)
NB toutes les inclusions sont au sens large, bien sûr
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 08 Aoû 2006, 10:32
par nada-top » 08 Aoû 2006, 10:32
bonjour Alben
c'est parfaitement claire maintenant :++:
merci :king2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
