Résoudre équation dans C

[mathieum13]

Salut,
sauriez vous m'indiquer comment trouver tous les nombre complexes z tels que
(z /(z-1))^4 soit réel.

Merci d'avance !

[Flodelarab]

Oui cherche séparement le module et l'argument de ton nombre final

[yos]

Je dirais une droite et trois cercles, privés de deux points

[B_J]

Salut
Ecartons le cas evident z=0
On a :
t=(z/(z-1))^4 reel arg(t) =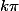
4[arg(z)-arg(z-1)] =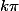
Or , A designant le point de Ox tel que OA=1 ( mesure algebrique) , on a
(mod ) :
arg(z)-arg(z-1)=(Ox,OM)-(Ox,AM)=(AM,OM) ...(angles de vecteurs)
On a donc :
t reel 4[(AM,OM)+]=
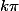
(MA,MO)=
En designant par B et B' les points de Oy tels que OB=-OB'=1 (mesures algebriques).
L'ensemble cherché est donc formé :
-de l'axe x'Ox , privé de A qui correspond a k=0
-du cercle de diametre OA privé de A qui correspond a k=2
-du cercle circonscrit au triangle OAB privé de A qui correspond a k=-1
-et du cercle circonscrit au triangle OAB' privé de A qui correspond a k=1