Résolution d'une série

[Chepmail]

Cherche super matheux pour résoudre une série particulièrement difficile.

y= (a*1)/n^2 *(1-1/n)*sin[(k*a*1)/n*(1-1/n)+(b*1)/n]+

[INDENT](a*2)/n^2 *(1-2/n)*sin[(k*a*2)/n*(1-2/n)+(b*2)/n]+

(a*3)/n^2 *(1-3/n)*sin[(k*a*3)/n*(1-3/n)+(b*3)/n]+

(a*4)/n^2 *(1-4/n)*sin[(k*a*4)/n*(1-4/n)+(b*4)/n]+

(a*5)/n^2 *(1-5/n)*sin[(k*a*5)/n*(1-5/n)+(b*5)/n]+

(a*6)/n^2 *(1-6/n)*sin[(k*a*6)/n*(1-6/n)+(b*6)/n]+

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

(a*(n-1))/n^2 *(1-((n-1))/n)*sin[(k*a*(n-1))/n*(1-((n-1))/n)+(b*(n-1))/n]+

(a*n)/n^2 *(1-n/n)*sin[(k*a*n)/n*(1-n/n)+(b*n)/n][/INDENT]

[adrien69]

Pour moi ça a une tronche de convergence type intégrale de Riemann (mais je ne pas en être sûr vu que je me perds dans ta présentation, tu peux pas l'écrire en LaTeX sous une forme plus compacte ? Avec un sigma pour k variant de blabla à blabla).
Essaie de voir ce que ça donne en comparant ta formule avec la formule générale de l'intégrale de Riemann.

[Robic]

Si j'ai bien compris, il s'agit de calculer la somme (et non la série) :



C'est bien ça ?

Quelle horreur !

Est-ce que ça provient d'un exercice, auquel cas on sait que le calcul est possible ? Ou bien est-ce que ça provient d'un TP, d'un projet ou je ne sais quoi, auquel cas il est fort possible que ça soit incalculable à la main (comme la majorité des problèmes concrets) ?

Cela dit, si c'était vraiment une série, il est facile de voir que si |a|<1 alors la série est absolument convergente, donc convergente. En effet, en valeur absolue le sinus machin est <=1 et |1-j/n|<= 1 (puisque j est compris entre 1 et n). Donc le terme général est, en valeur absolue, inférieur à |a^j|, dont la série converge si |a|<1 (série géométrique).

[adrien69]

Je pense que c'est j.a au départ, pas de puissance
Donc ici Riemann marche très bien en fait.
C'est a priori:


Ce que je refuse tout bonnement de calculer.

[Chepmail]

Si j'ai bien compris, il s'agit de calculer la somme (et non la série) :



C'est bien ça ?

Quelle horreur !

Est-ce que ça provient d'un exercice, auquel cas on sait que le calcul est possible ? Ou bien est-ce que ça provient d'un TP, d'un projet ou je ne sais quoi, auquel cas il est fort possible que ça soit incalculable à la main (comme la majorité des problèmes concrets) ?

Cela dit, si c'était vraiment une série, il est facile de voir que si |a|<1 alors la série est absolument convergente, donc convergente. En effet, en valeur absolue le sinus machin est <=1 et |1-j/n|<= 1 (puisque j est compris entre 1 et n). Donc le terme général est, en valeur absolue, inférieur à |a^j|, dont la série converge si |a|<1 (série géométrique).

Bonjour,
La formule est bonne. Il s'agit du résultat de l'évolution de molécules. Il ne s'agit pas d'un cas d'école mais d'une réalité physique. Il n'y a peut-être pas de solution, hormis l'itération sur ordinateur.
Bon courage.
André

[Robic]

Pourquoi « bon courage » ? Tu crois que quelqu'un va essayer de calculer cette abomination ? :lol3:

Plus sérieusement, puisque c'est un vrai problème concret, je crains que ce soit incalculable à la main et à mon avis personne ne va vouloir essayer (on n'est pas des bêtes...)

[adrien69]

Pourquoi « bon courage » ? Tu crois que quelqu'un va essayer de calculer cette abomination ? :lol3:

Plus sérieusement, puisque c'est un vrai problème concret, je crains que ce soit incalculable à la main et à mon avis personne ne va vouloir essayer (on n'est pas des bêtes...)

En vrai je pense que ça se calcule comme une intégrale de Wallis, mais merde, j'ai dépassé la Sup' depuis trop longtemps. :zen:

[adrien69]

Bonjour,
La formule est bonne. Il s'agit du résultat de l'évolution de molécules. Il ne s'agit pas d'un cas d'école mais d'une réalité physique. Il n'y a peut-être pas de solution, hormis l'itération sur ordinateur.
Bon courage.
André

Attends, c'est ou ??
Ça changerait tout.
Surtout que si a est un paramètre qui a une dimension c'est un calcul absurde dans le cas où c'est .

[deltab]

Bonjour
La formule est exacte, approchée?

Peut-on assimiler à (ordre de grandeur de n,a,k et b). Si oui on pourra peut-être simplifier la somme

[adrien69]

Mais d'après ce qu'il a dit au départ c'est pas !!!

[deltab]

Bonjour.

il a bien écrit (a*1)/n^2, (a*2)/n^2,....,(a*(n-1))/n^2, (a*n)/n^2 dans la longue expression qu'il donnée, il s'agit de et non .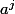
Si on peut faire l'assimilation citée plus haut, la somme peut être effectivement simplifiée avec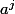 ou et si je n'ai pas fait d'erreur, on se ramène pour à calculer pour qui sont des polynômes de degré p+1

[adrien69]

Mais si c'est aj, j'ai déjà donné la réponse........... :mur:
C'est une somme de Riemann, pas besoin de simplifier quoi que ce soit...

[deltab]

Bonjour

Mais si c'est aj, j'ai déjà donné la réponse........... :mur:
C'est une somme de Riemann, pas besoin de simplifier quoi que ce soit...

dont la limite est , ce que tu as refuse tout bonnement de calculer.

Si l'assimilation est possible, la nouvelle somme est encore une somme de Riemann dont la limite est
qui se calcule aisément.