Resolution d'une equation de type sinusoidale

[yokute]

Bonjour,

Mes cours de mathématique sont un peu ancien et je cherche a trouver tel que:


Avec
,



Vous trouverez ci-dessous le tracer de:



pour:





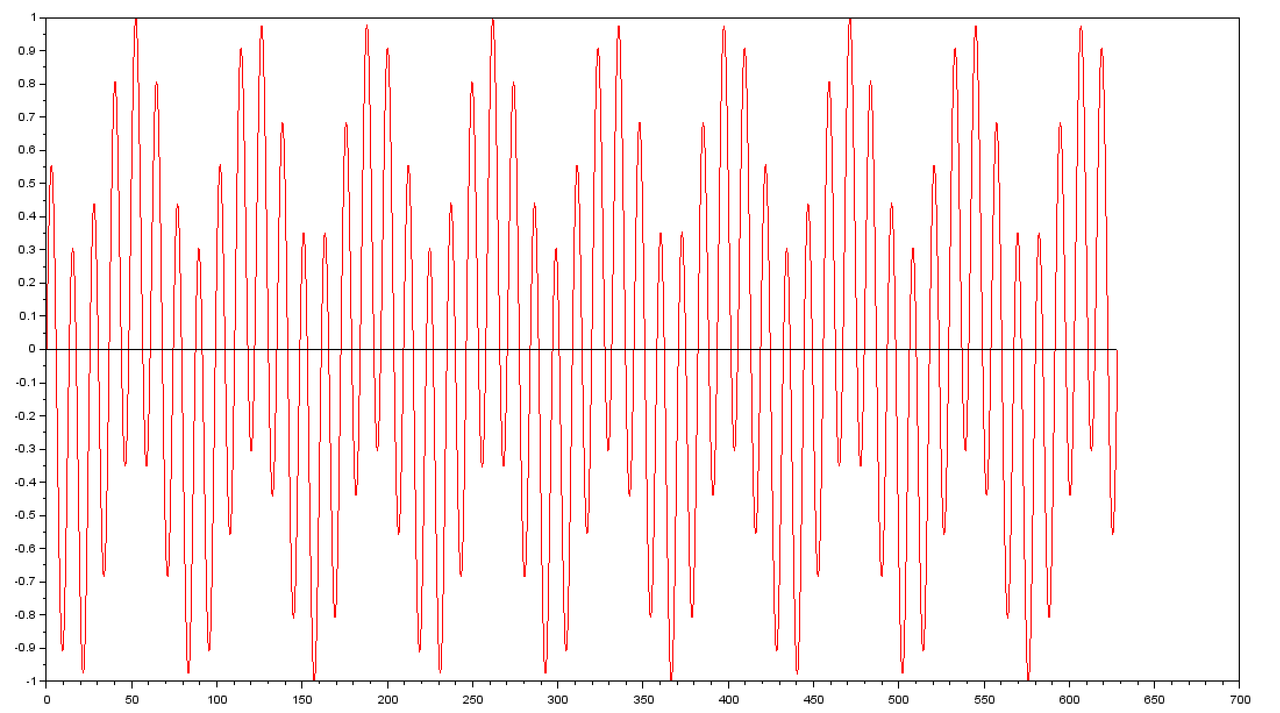
Comme vous pouvez le constater il y a une infinité de solutions. Je suis surtout intéresser par le plus petit réel positif.

J'ai essayé de trouver la solution avec "SAGE", je n'y arrive pas.

Je suis bien évidement intéressé par la méthode et pas seulement la solution car j'aurai d'autre cas similaires.

Merci d'avance pour votre aide

[GaBuZoMeu]

Que cherches-tu exactement ?
Une "formule" te donnant (la plus petite solution positive) en fonction de et ? Là, je suis persuadé qu'il n'y a aucun espoir d'en obtenir une.
Un moyen d'obtenir numériquement cette plus petite solution positive pour et donnés ? Là, SageMath peut très certainement faire ça.

[yokute]

Salut,
Oui je cherche une fonction de r et x me donnant le plus petit n positif tel que l'équation ci dessus soit vérifiée. J'arrive déjà à trouver numériquement une solution mais j'aurais aimé avoir une fonction.

[GaBuZoMeu]

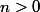
Il y a une fonction, c'est sûr : la fonction qui à associe le plus petit tel que .
Mais ce dont je suis à 99,99% sûr, c'est que cette fonction ne s'exprime pas au moyen des fonctions élémentaires (celles que tu as eu l'occasion de rencontrer, disons).

[Ben314]

Salut,
Après, la question c'est de savoir pourquoi tu voudrait avoir l'expression de r(n,x) exprimé à l'aide des fonctions usuelles. Si c'est pour une quelconque application pratique ça n'a pas vraiment d'intérêt vu qu'avec n'importe quel langage de programmation (pas trop bidon) tu peut avoir une approximation aussi précise (et presque aussi rapide) que celle que tu as par exemple lorsque tu demande au même langage de calculer une formule compliquée contenant des fonction transcendantes (sin, cos, exp, log). Et si c'est pour un calcul théorique, ben tu fait ce que dit GaBuZoMeu, à savoir que tu donne un nom à la fonction en question et que tu continue tes pérégrinations théoriques en utilisant ce nom là : il faut bien comprendre que c'est ce qu'on fait les premiers à utiliser des fonctions comme l'exponentielle, le log ou la fonction gamma avant que ça ne devienne des "fonctions usuelles".

[yokute]

Merci pour vos réponses, c'est juste que cela aurait plus confortable pour interpréter le résultat et le comparer avec les autres fonctions que je vais trouver. Et surtout pour voir si je peux généraliser le résultat avec mes autres cas. Mais je vais continuer avec des abaques.
Merci encore