Resolution system de 2 equations a 2 inconues
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Palpale
- Messages: 2
- Enregistré le: 23 Avr 2020, 08:23
-
 par Palpale » 23 Avr 2020, 09:04
par Palpale » 23 Avr 2020, 09:04
Bonjour !
Dans le cadre de mon stage je dois résoudre un system de 2 équations a 2 inconnues que vous trouverez dans la photo ci-dessous (31). Plus particulièrement j'aimerai trouver le moyen d'arriver au polynome en

que vous trouverez également sur la photo (32).
Les inconnues sont

toutes les autres variables sont connues et réelles. De plus


J'ai déjà essayé de développer les 2 équations pour n'avoir qu'une seule variable dans les cos et sin. En prenant ensuite
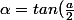, \beta = tan(\frac{b}{2}))
et en remplaçant
 = \frac{1-\alpha^2}{1+\alpha^2}, cos(b) = \frac{1-\beta^2}{1+\beta^2}, sin(a) =\frac{2*\alpha}{1+\alpha^2}, sin(b) =\frac{2*\beta}{1+\beta^2})
on obtient toujours un système de 2 équations à 2 inconues mais cette fois ci polynomial. Le problème c'est que je n'arrive pas à trouver la simplification qui mène à l'équation (32).
Une petite aide serait super sympa !

-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 23 Avr 2020, 10:07
par GaBuZoMeu » 23 Avr 2020, 10:07
Tu as deux équations polynomiales en

. Tu peux éliminer
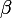
entre les deux équations et obtenir une seule équation polynomiale en
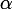
en utilisant le résultant des deux polynômes par rapport à
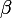
.
Sur la toile, tu as
l'article wikipedia sur le résultant. Mais il y a aussi plein d'autres ressources en ligne.
J'espère pour toi que tu utilises un système de calcul formel. Il a alors à coup sûr une commande "résultant".
Quoique, à la vue du résultat, le résultant se calcule peut-être facilement à la main. Il faudrait voir les deux équations en

.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 23 Avr 2020, 11:55
par Pisigma » 23 Avr 2020, 11:55
Bonjour,
autre piste , peut-être, écrire le système sous la forme
 +l_i\, cos(a-b-\Phi_i)-sin(a-b)=O_{jx})
 -l_i\, sin(a-b-\Phi_i)-cos(a-b)=O_{jy}+1)
ensuite élever au carré et ajouter membre à membre; simplifier l'expression obtenue
et à ce moment utiliser les changements de variables
-
Palpale
- Messages: 2
- Enregistré le: 23 Avr 2020, 08:23
-
 par Palpale » 23 Avr 2020, 13:17
par Palpale » 23 Avr 2020, 13:17
Bonjour,
Merci beaucoup pour vos réponses rapides. Je ne connaissais pas du tout le résultant de deux polynômes, je me coucherai moins bête ! Je vais creuser vos 2 pistes.
Bonne journée !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités


