Résolution rapide d'équation.

[ACatToTheMoon]

Bonjour,
J'aimerais avoir la façon la plus simple et rapide, avec le moins de lignes de calculs possible pour trouver x en résolvant racine de K = 1+x/1-x. Je sais le faire mais je trouve ma méthode un peu longue.
Merci par avance.

[Ben314]

Salut,
, ça fait 1 en permanence, donc y'a rien à résoudre.


EDIT (je viens de voir ton papier) : je comprend pas comment on peut se retrouver dans le "supérieur" sans même avoir acquis les bases élémentaires du calcul vu en sixième.
Les multiplication/divisions sont prioritaires sur les additions/soustractions.
1+x/1-x, normalement, on apprend en sixième que ça veut dire 1+(x/1)-x et pas autre chose !!!!

[ACatToTheMoon]

J'ai oublié les parenthèses dans mon message, je voulais dire (1+x)/(1-x), en fait comme marqué sur la première ligne du papier... Je sais très bien que les multiplications et les divisions étaient prioritaires... J'ai juste fait une erreur de notation dans mon message.

[Ben314]

Bon, sinon, je te rédige le truc correctement :
Pour positif fixé, on cherche tel que .
La "logique" de résolution (vue au collège), c'est de retrancher un des deux membres de l'équation des deux cotés de façon à avoir truc=0 puis à factoriser truc de façon à pouvoir dire qu'un produit de facteurs est nul ssi un des facteurs est nul.

une fraction est nulle ssi son numérateur est nul et son dénominateur est non nul (toujours niveau collège...)
(car ne peut jamais être nul vu que )
Ensuite, il faut évidement regarder à quelle condition est différent de 1 :
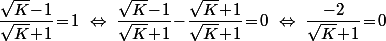
ce qui est impossible.

Donc, quelque soit , l'unique solution de l'équation est (qui est systématiquement différent de 1).

[ACatToTheMoon]

Super, merci.