Résolution équation

[ptit_seb]

Bonsoir,

Voici l'intitulé simplifié du problème que l'on me pose:

Soit l'équation x1+x2^2+x3^3+x4^4+2*x5+2*x6^2+2*x7^3+2*x8^4=y
Soit x1 à x8 défini en 0 et 35

Définir le nombre y ayant le plus grand nombre de solutions possible (500Enoncé les 20 premières série de chiffre de x1 à x8 permettant de vérifier l'équation.

Je ne trouve pas de solution.

Une idée?

Merci pour vos posts

[redwolf]

et doit être compris entre 500 et 5000. Je suppose que tous les nombres qui interviennent sont des entiers.

Déjà, car .
De même, on voit que , et .

Avec ça, il n'y a déjà plus que 30 milliards de possibilités à tester.

Tu es sur que ce n'est pas plutôt un exercice d'informatique ? Un petit programme pourrait peut-être nous donner la réponse assez rapidement ?

[ptit_seb]

et doit être compris entre 500 et 5000. Je suppose que tous les nombres qui interviennent sont des entiers.

Déjà, car .
De même, on voit que , et .

Avec ça, il n'y a déjà plus que 30 milliards de possibilités à tester.

Tu es sur que ce n'est pas plutôt un exercice d'informatique ? Un petit programme pourrait peut-être nous donner la réponse assez rapidement ?

En fait si, mais étant nul en programmation et étant plus un problème de mathématique, je pensé trouver des pistes ou des réponses :we:

[redwolf]

Déjà, je rectifie, c'est qui est >5000.

Maintenant, je vais programmer ça...

[ptit_seb]

Déjà, je rectifie, c'est qui est >5000.

Maintenant, je vais programmer ça...

Si tu arrive à programmer un algorthyme ou un logciel cela je t'en serais vraiment reconnaissant et cela m'aiderais grandemant.

Mais je pense mettre mal exprimer dans l'énoncé de mon problème :
l'équation est bonne mais en fait je recherche le nombre y (500<y<5000 venait d'un autre problème :marteau: désolé)
y doit être le nombre autorisant le plus grand nombre de réponse possible de la part de x1 à x8 ou x1 à x8 sont des nombres entier entre 0 et 35.

Merci pour tes réponses

[babulle]

est-ce que par hazard, il ne s'agirait pas d'un TP d'info noté ?

[ptit_seb]

nan en fait c'est pour un projet personnelle que je souhaite implanté dans un programme existant.

C'est une équation que j'ai écrite pour un besoin précis.
Mais au final il faudrait que j'avrrive à le convertir en programme afin de pouvoir déterminer les différents X en fonction d'un y.
Mais je ne possède pas de valeur y pour le moment.

Et comme je suis relativement nul en algorythme et en programmation....

Je demande de l'aide ici

Mais au vue des réponses plus hautes (je n'attendais pas autant de possiblités), je souhaite modifié l'équation pour donner
x1+x2^2+x3^3+2*x+2*x5^2+2*x6^3=y avec des x en nombre entier de 0 à 35.

Pouvez vous m'aider ?

[redwolf]

Et voici la glorieuse réponse au premier problème posé (même si l'énoncé a été modifié depuis...) :

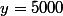
C'est qui admet le plus grand nombre de représentations de la forme souhaitée.

Il y en a très exactement : 3772262

Mais comme je suis sans doute bien plus nul encore que toi en programmation, je vais te laisser écrire tes propres algorithmes.

Le seul conseil que je peux donner, c'est de décomposer le problème comme suit (je prends maintenant le nouvel énoncé) :
Etudie d'abord le nombre de représentations d'un entier sous la forme
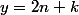
. Ensuite, pour chaque écriture de sous la forme , tu as représentations de sous la forme souhaitée.

Bon courage...

[redwolf]

Pour le nouvel énoncé, c'est 2282 le grand champion. Il possède 78447 représentations de la forme .
Son voisin 2280 n'est pas mal non plus, avec 78445 représentations.

[ptit_seb]

Merci pour ce chiffre y et le nombre de solution possible avec les x.
sa m'aide déjà grandement.

Peut tu m'expliquer tes calculs ou mes les transmettres par mail ?