Résolution équation fonctionnelle, Laplace
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nicr
- Messages: 6
- Enregistré le: 15 Mai 2009, 15:51
-
par nicr » 19 Nov 2009, 15:03
Bonjour tout le monde, :id:
Je dois expliciter la méthode d'un auteur permettant de trouver une fonction inconnue
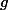
sous intégrale dans l'équation suivante :
 = \frac{3R}{p\tau^2} \sum_{n=1}^{\infty} n \int_0^{\infty} t^2 g(t) e^{\frac{-nt}{\tau}} dt)
Il a écrit que :
 = \frac{2p}{\pi t^2} \sum_{m=1}^{\infty} \frac{a_m}{m} (1-\cos(m t)))
"parce que cette forme de la transformée de Laplace est pratique." Sauriez-vous comment il peut avoir trouvé cette fonction
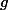
s'il vous plaît ?
Je serais vraiment très très très heureux de votre aide ! :id:
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
par kazeriahm » 19 Nov 2009, 15:38
C'est quoi a_m par rapport a gamma ?
-
nicr
- Messages: 6
- Enregistré le: 15 Mai 2009, 15:51
-
par nicr » 19 Nov 2009, 19:51
a_m est une constante qui dépend sûrement de gamma, mais peu m'importe comment.
par alavacommejetepousse » 19 Nov 2009, 20:24
bonsoir
sans rien écrre
je dirais qu 'il a rentré la somme dans l'intégrale calculé la somme et utilisé la transformée inverse
-
nicr
- Messages: 6
- Enregistré le: 15 Mai 2009, 15:51
-
par nicr » 21 Nov 2009, 11:02
:we: Merci beaucoup kazeriahm et alavacommejetepousse. :we:
Comme $g$ est inconnue, ça veut dire qu'on peut trouver cette forme générale pour une fonction $g$ quelconque juste en utilisant Laplace inverse appliqué à la somme ? :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
