Résolution d'équation différentielle et détermination de l'é

[HERCOLUBUS]

Soit:



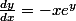
Résoudre cette équation différentielle et par la suite, déterminer l'équation de la courbe qui passe par P(0,1).

Quelle est la démarche à suivre ? :hein:

[jlb]

variables sésparées -e^(-y)dy=xdx tu intègres membre à membre et tu as ta solution à partir de la condition initiale.

[HERCOLUBUS]

variables sésparées -e^(-y)dy=xdx tu intègres membre à membre et tu as ta solution à partir de la condition initiale.

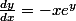
En isolant les variables de chaque coté de l'équation , j'obtiens:



Ce qui ensuite devient:



En intégrant les 2 membres de l'équation je trouve:



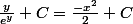
Ensuite, qu'elle variable dois-je exprimée en fonction de l'autre pour trouver l'équation de la courbe qui passe par P(0,1) ????

[JeanJ]

Erreur : y/exp(y) n'est pas une primitive de 1/exp(y)

[Black Jack]

dy/dx = -x.e^y

e^-y dy = -x dx

-e^-y = -x²/2 - K
e^-y = x²/2 + K
e^y = 1/(x²/2 + K)

y = -ln(x²/2 + K)

Passe par (0,1) ---> 1 = -ln(K)
K = 1/e

y = -ln(x²/2 + 1/e)

:zen:

[HERCOLUBUS]

dy/dx = -x.e^y

e^-y dy = -x dx

-e^-y = -x²/2 - K
e^-y = x²/2 + K
e^y = 1/(x²/2 + K)

y = -ln(x²/2 + K)

Passe par (0,1) ---> 1 = -ln(K)
K = 1/e

y = -ln(x²/2 + 1/e)

:zen:

Wow merci Black Jack