Résolution equa diff

[bipbip8]

Bonjour,
Pour un besoin technique, j’ai besoin de résoudre l’équation différentielle suivante :

Avec U_0 , L , w et R des constantes positives
J’ai cherché sur le net mais en vain.
Merci d’avance pour votre aide.

[lionel52]

Salut pour avoir l'ensemble des solutions tu utilises la méthode de variation des constantes.
Soit z0 = exp(-Rt/L), une solution de l'équation homogène R.i + Ldi/dt = 0.

Si tu poses y = z0.z une solution de l'équation d'origine alors on remarque que z doit vérifier

Lz0.z' = |U0.sin(wt)| Donc

et

[paquito]

C'est une équation différentielle d'ordre un avec un second membre continu, donc élémentaire; le second membre désigne la tension injectée dans un circuit , la tension au bornes du résistor est bien
sûr égale à et la tension aux bornes de la bobine est, la valeur absolu désigne de l'alternatif redressé. Recherche une solution particulière sous la forme
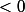
d'abord pour puis; Je ne pense pas que Laplace donne quelque chose et si ça ne marche pas développe le second membre en série de Fourier. désolé, ais je n'ai pas le temps de le faire.