bonjour,
j'ai un probleme pour resoudre cette equation du premier ordre j'ai applique la methode des caracteristiques mais si je fais la verification apres sa ne tombe pas juste....
Ut+xUx=x t>0, x>0
U(0,t)=0
U(x,0)=0
Resolution EDP
9 messages
- Page 1 sur 1
Re: Resolution EDP
Bonjour
Peux tu écrire ton équation exactement pour être sûr du problème ? D'autre part, donne ta solution pour voir.
Peux tu écrire ton équation exactement pour être sûr du problème ? D'autre part, donne ta solution pour voir.
Re: Resolution EDP
Les caractéristiques donnent 2 équations différentielles indépendantes, soit 2 constantes arbitraires (ici notées  et
et  ). On exprime les solutions sous forme
). On exprime les solutions sous forme 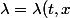) et
et 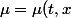)
Si ton cours est correct, il doit préciser que la solution s'écrit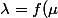) ,
,  étant une fonction arbitraire
étant une fonction arbitraire
Si ton cours est correct, il doit préciser que la solution s'écrit
Re: Resolution EDP
Bonjour je viens de voir la réponse de Pythales alors que j'allais donner quelques explications mais comme ce n'est pas forcément redondant je les donne:
une caractéristique est donnée par l'équation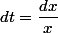 dont les solutions sont de la forme
dont les solutions sont de la forme 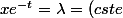.)
Sur une telle caractéristique la solution vérifie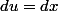 donc
donc 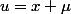 où
où  est une constante sur cette caractéristique, c'est à dire que cela ne dépend que de
est une constante sur cette caractéristique, c'est à dire que cela ne dépend que de  ; c'est une fonction de
; c'est une fonction de 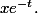 En désignant par
En désignant par  cette fonction on arrive au résultat
cette fonction on arrive au résultat
une caractéristique est donnée par l'équation
Sur une telle caractéristique la solution vérifie
Re: Resolution EDP
Bonjour
j'ai compris cette démarche mais je vérifie les conditions aux limites je ne trouve pas zéro
j'ai compris cette démarche mais je vérifie les conditions aux limites je ne trouve pas zéro
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
