Résolu - Merci
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
fioldodidi
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Oct 2017, 15:44
-
 par fioldodidi » 11 Jan 2018, 07:09
par fioldodidi » 11 Jan 2018, 07:09
Bonjour,

J'ai réussi à prouver que
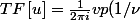+\frac{1}{2}\delta)
avec u : échelon d'Heaviside.
Mais je dois maintenant en déduire que
]=\pi i({u(\nu)-u(-\nu)}))
et
-u(-\nu)}{2})
Pouvez vous m'aider ?
Merci !
Modifié en dernier par
fioldodidi le 11 Jan 2018, 17:04, modifié 1 fois.
-
aviateur
 par aviateur » 11 Jan 2018, 13:23
par aviateur » 11 Jan 2018, 13:23
Bonjour pour les notations j'utilise ici: variable x pour une fonction h et y pour sa transformée de Fourier H
Posons g(x)=vp(1/x)
On a donc
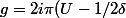.)
On sait que F(\delta)=1.
Calculons F(U): F(U) (y) =F^{-1} (U) (-y)= F^{-1} (F(u))(-y)=u(-y) .
Il vient donc
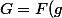= (2 i \pi) (u(-y) -1/2 ))
d'où le résultat.
Pour le dernier résultat il suffit d'utiliser la propriété qui relie Fourier de la dérivée d'une fonction (ou distribution) T
avec la transformée de Fourier de T
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités