Dm de reprise
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
grosedpichet
- Membre Naturel
- Messages: 13
- Enregistré le: 02 Sep 2010, 18:48
-
 par grosedpichet » 02 Sep 2010, 19:03
par grosedpichet » 02 Sep 2010, 19:03
Bonjour je reprends actuellement les cours et j'ai un dm de maths à faire.
Or j'ai un blocage peut etre du au 2mois de vacance sur une question/demonstration au niveau des nombres complexes :
enoncé : Dans un plan complexe muni du repère orthonormal (O;u;v), on considère les point M et M' d'affixes respectives z et z'. On pose z=x+iy et z'=x'+iy'.
1 montrer que les vecteurs OM et OM' sont orthogonaux si et seulement si Re(z'*zbar)=0 zbar==> conjugué de z
2 Montrer que les points 0, M et M' sont alignés si et seulement si Im(z'*zbar)=0
Voila si vous pouviez m'aider merci :we:
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 02 Sep 2010, 19:05
par windows7 » 02 Sep 2010, 19:05
ca te parle les determinants ?
-
grosedpichet
- Membre Naturel
- Messages: 13
- Enregistré le: 02 Sep 2010, 18:48
-
 par grosedpichet » 02 Sep 2010, 19:06
par grosedpichet » 02 Sep 2010, 19:06
C'est à dire ? c'est un exo de reprise de PCSI donc c'est forcement sur le programme de term etant donné que je n'ai pas encore fait de cours de prepa !

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 02 Sep 2010, 19:15
par Sa Majesté » 02 Sep 2010, 19:15
Salut
Calcule

en fonction de x, x', y et y'
-
grosedpichet
- Membre Naturel
- Messages: 13
- Enregistré le: 02 Sep 2010, 18:48
-
 par grosedpichet » 02 Sep 2010, 19:21
par grosedpichet » 02 Sep 2010, 19:21
oui celà donne xx'+yy'-i(x'y-xy') ?
à quoi ça peut servir ?
sa partie reelle est donc xx'+yy' et non 0

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 02 Sep 2010, 19:26
par Sa Majesté » 02 Sep 2010, 19:26
Que peux-tu dire de 2 vecteurs orthogonaux ?
-
grosedpichet
- Membre Naturel
- Messages: 13
- Enregistré le: 02 Sep 2010, 18:48
-
 par grosedpichet » 02 Sep 2010, 19:29
par grosedpichet » 02 Sep 2010, 19:29
Que leur produit est egal à 0 !

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 02 Sep 2010, 19:33
par Olympus » 02 Sep 2010, 19:33
Tu peux passer par le produit scalaire aussi :
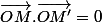
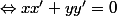
 = 0)
 = 0)
EDIT pour au-dessus : plutôt "produit scalaire" et pas "produit" .
EDIT 2 : grillé par Sa Majesté :briques:

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 02 Sep 2010, 19:42
par Sa Majesté » 02 Sep 2010, 19:42
Oui c'est ça, je voulais te faire penser au produit scalaire
Et comme tu as un repère ...
-
grosedpichet
- Membre Naturel
- Messages: 13
- Enregistré le: 02 Sep 2010, 18:48
-
 par grosedpichet » 02 Sep 2010, 19:55
par grosedpichet » 02 Sep 2010, 19:55
oui je comprends tout à fait mais le produit scalaire OM.OM' n'est pas egal à xx'+yy' mais à xx'+yy'+i(xy'+x'y) et c'est Re(z'*zbar)=xx'+yy' alors voilà je ne comprends pas

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 02 Sep 2010, 19:58
par Sa Majesté » 02 Sep 2010, 19:58
grosedpichet a écrit:oui je comprends tout à fait mais le produit scalaire OM.OM' n'est pas egal à xx'+yy' mais à xx'+yy'+i(xy'+x'y)
Il faut revoir ton cours de toute urgence :briques:
Le produit scalaire est bien égal à xx'+yy'
-
grosedpichet
- Membre Naturel
- Messages: 13
- Enregistré le: 02 Sep 2010, 18:48
-
 par grosedpichet » 02 Sep 2010, 20:20
par grosedpichet » 02 Sep 2010, 20:20
oula merci ^^
-
grosedpichet
- Membre Naturel
- Messages: 13
- Enregistré le: 02 Sep 2010, 18:48
-
 par grosedpichet » 02 Sep 2010, 20:27
par grosedpichet » 02 Sep 2010, 20:27
mais pour la question 2 du coup je comprends toujours pas =S

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 02 Sep 2010, 20:43
par Sa Majesté » 02 Sep 2010, 20:43
C'est pareil que le 1 si tu as vu le produit vectoriel
Sinon O, M et M' sont alignés ssi il existe k réel tq
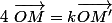
-
grosedpichet
- Membre Naturel
- Messages: 13
- Enregistré le: 02 Sep 2010, 18:48
-
 par grosedpichet » 02 Sep 2010, 20:57
par grosedpichet » 02 Sep 2010, 20:57
oui pour les vecteurs colineaires ok ca je l'avais déjà marqué sur mon brouillon exactement ce que tu viens d'ecrire mais après Im(z'*zbar)=i(-x'y+xy') et le probleme c'est comment y parvenir en partant de OM=kOm'

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 02 Sep 2010, 21:06
par Sa Majesté » 02 Sep 2010, 21:06
Tu passes aux coordonnées
x = kx'
y = ky'
-
grosedpichet
- Membre Naturel
- Messages: 13
- Enregistré le: 02 Sep 2010, 18:48
-
 par grosedpichet » 02 Sep 2010, 21:43
par grosedpichet » 02 Sep 2010, 21:43
:hein: je vois toujours pas ...

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 02 Sep 2010, 23:28
par Olympus » 02 Sep 2010, 23:28
Pour la question 2, fais comme ce qu'on vient de faire avec la question 1 : travaille en géométrie analytique avec les deux points M(x;y) et M'(x';y'), en oubliant totalement les complexes . Une fois trouvé la condition suffisante et nécessaire sur x,x',y,y' pour que O, M et M' soient alignés, tu passes aux complexes .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
