[Résolu] Représenter un plan dans l'espace

[Zayaan]

Bonjour ! Travaillant sur un programme de représentation de molécules dans l'espace, me voilà face au problème suivant :

J'ai un plan d'équation ax+by+cz+d=0. Je peux donc projeter tous les points de ma molécule sur ce plan.

J'aimerais trouver les coordonnées de 4 points correspondant aux 4 sommets d'un rectangle tel qu'il soit sur mon plan et qu'il contienne toutes les projections de mes points de la molécule.

J'ai les coordonnées de mes projections (x,y,z)(dans le repère spatial), l'équation du plan, mais ne sais comment poursuivre, n'étant pas très connaisseur de telles manipulations de coordonnées. Quelqu'un pourrait-il me mettre sur la voie, ou aurait-il une idée qui pourrait me permettre d'avancer ?

Merci par avance :)

[yos]

Une des raisons de la difficulté est qu'il y a une infinité de rectangles qui marchent.
Tu peux imposer une contrainte supplémentaire comme "deux côtés du rectangle sont parallèles au plan (Oxy)". Les points projetés dont la cote est minimum et ceux dont la cote est maximum te donnent les deux côtés en question.
Tu peux recommencer avec le plan (Oxz) et tu as deux autres côtés ... d'un parallélogramme.

[Zayaan]

Alors, après quelques essais, je ne suis pas sûr d'avoir compris ton indication : en effet, si je détermine que les côtés de mon rectangle (ou parallélogramme, le critère rectangulaire n'est pas si important) doivent être parallèles aux axes de mon espace, je sors alors de mon plan, qui lui n'est parallèle ni à (0xy), (0xz) ou (0yz).

Si on part sur l'idée que le parallélogramme doit avoir une taille minimale (ce qui ajoute une contrainte supplémentaire qui pourrait être utile), englobant toutes les projections, il ne devrait y avoir qu'une seule figure possible, non ?

Je peux effectivement me baser sur les projections "extrêmes", que tu sembles déterminer par la "cote" des points. Je ne connais pas cette propriété, quelle est-elle ?

Si on arrive à trouver les projections "extremes" qui délimitent la projection de la molécule, les bords de mon parallélogramme devraient passer par ces projections, mais comment les orienter correctement, et déterminer les coordonnées de leurs "croisements" qui devraient être celles des sommets du parallélogramme ?

Beaucoup de questions, je suis navré, je n'ai pas grande connaissances de la géométrie dans l'espace. Merci en tout cas de ta réponse qui m'a donné la piste des "projections délimitatrices", je vais continuer à creuser dans ce sens.

[skilveg]

Ce que tu peux faire aussi, c'est projeter d'abord tes points, envoyer le plan de projection sur le plan 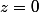par une transformation affine, et choisir ensuite un rectangle de ce plan qui convienne (par exemple un rectangle aux côtés parallèles aux axes). Ce dernier choix n'est pas trop dur puisque tu as les nouvelles coordonnées des points projetés, et tu peux regarder celles d'abscisse (resp. d'ordonnée) minimales et maximales.

[Zayaan]

Cette dernière solution me semble plus simple, effectivement. Si j'ai bien compris, je projette mes points sur le plan z=0, je trouve les coordonnées de mon rectangle délimiteur, et je le reprojette sur mon plan de projection ? Je vais essayer de faire cela :)

[skilveg]

Non non; si j'ai bien compris ton but c'est de faire bouger le plan sur lequel tu projette pour mieux voir la forme de la molécule non? dans ce cas voilà ce que je ferais, en un peu plus détaillé que tout à l'heure :

- ton plan est donné par 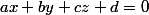. Je projette orthogonalement tous les points sur , et j'en choisis un en particulier, appelons-le .

- je soustrais à toutes les coordonnées: maintenant le plan qui nous intéresse passe par l'origine. En plus on a un vecteur normal de ce nouveau plan, c'est .

- je détermine une rotation qui envoie ce vecteur sur un vecteur positivement colinéaire à 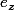; on doit pouvoir le faire matriciellement sans trop de problèmes.

- j'applique à toute la figure; maintenant le nuage de points est dans le plan .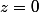

- enfin, il ne reste plus qu'à choisir un bon rectangle qui contienne tous tes points.

Tu peux aussi utiliser des projections stéréographiques pour observer ta molécule, mais je ne m'y connais pas trop...

[Zayaan]

Navré si mes explications étaient confuses, il me semble qu'on s'est mal compris : je veux juste réussir à "dessiner" le plan sur lequel je projette ma molécule, donc dessiner un rectangle qui le représente et qui contient toutes les projections. Ainsi, les points ne doivent pas bouger, et le plan ne peut pas changer non plus. Or, d'après ton explication, je me base sur le plan z=0 sur lequel je calque mon plan de projection, et bouge ma molécule afin que tout concorde ? Je souhaite garder mon plan d'origine.

J'ai commencé à essayer la technique précédente que je croyais avoir comprise de ton explication, ça m'a l'air en bonne voie : j'ai les points de ma molécule dans l'espace, je les projette sur le plan z=0, je détermine les points "extrêmes", je trace le rectangle sur z=0 puis je projette le rectangle sur le plan de projection. Le rectangle projetté sur le plan de projection devrait bien contenir les points de la molécule projettée sur le même plan, non ?

Désolé s'il y a eu confusion d'idées, je vais aller manger puis relire à nouveau tout cela à tête reposée. Merci en tout cas de ton aide à réflexion, ça me permet d'avancer sur ce fichu problème, on va y arriver !

[Zayaan]

Alors, j'y suis presque :)

D'après la méthode expliquée précédemment, j'arrive à avoir un rectangle sur mon plan, de surface apparemment correcte.

Seul souci, il n'est pas au bon endroit du plan, ne "recouvre" donc pas les projections des points de la molécule. Disons que j'ai mes projections des points de la molécule à un endroit du plan, et mon rectangle à un autre. Voilà ma démarche :

Soit le plan z=0. Pour chaque atome de la molécule, on le projette sur le plan z=0. On cherche le xmin, xmax, ymin, ymax de cet ensemble de points. On détermine les coins du rectangle englobant tous ces points, soit les 4 points suivants : (xmin, ymin), (xmin, ymax), (xmax, ymax) et (xmax, ymin). Puis on projette ces 4 points sur mon plan de projection (qui est mon plan ax+by+cz+d=0).

Seul souci donc, le rectangle n'est pas du tout à l'endroit de la projection des points de la molécule sur ax+by+cz+d=0. Pourtant, la transformation est la même ! J'y suis presque, mais j'avoue ne pas comprendre cette incohérence ?

[Zayaan]

Trouvé ! Les projections étant perpendiculaires au plan initial, normal que la projection du plan z=0 vers le plan ax+by+cz+d=0 ne retombe pas sur les projections initiales de ma molécule :)

Dernière question et j'aurai fini : J'ai mes coordonnées des 4 coins du rectangle d'une part, et les coordonnées d'un nouveau point. Comment trouver les nouvelles coordonnées du rectangle telles que le nouveau point en soit le centre ? Il suffirait de faire une translation suivant le plan, tel que le centre du nouveau rectangle se confonde avec mon nouveau point, mais je ne sais comment faire la translation en question?

[skilveg]

Ainsi, les points ne doivent pas bouger, et le plan ne peut pas changer non plus.

Tu sais, en principe quand on fait des calculs, ça ne détruit pas les variables... Quand je parle de projection je veux plutôt dire "on calcule de nouveaux points qui sont les images des anciens". Et ce que je racontais tout à l'heure marche: si tu veux à tout prix remettre les points sur le plan , tu peux toujours appliquer l'inverse de la rotation puis l'inverse de la translation.

Pour ce qui est de ta dernière question, je ne vois pas bien où est le problème: ce que tu dis donne la solution (translater chacun des coins du même vecteur voulu). Bon, après, tu n'auras a priori plus tous les points dans le rectangle.

Bon courage pour la suite...

PS: en projetant d'abord sur le plan il me semble que tu perds l'intérêt de partir d'un plan arbitraire, mais bon...

[Zayaan]

Pour ton post scriptum, justement, le plan choisi n'est pas arbitraire, et bien défini (une propriété intrinsèque à la molécule), voilà pourquoi je désire travailler sur ce plan uniquement ;) Mais en effet, il aurait suffi d'appliquer l'inverse des transformations pour retourner sur le plan initial, je n'y avais même pas pensé...

Pour ma dernière question, j'ai réussi à faire ma translation, et c'est bon, j'ai mon joli rectangle tel que je le voulais :)
Merci beaucoup de ton aide, même si je n'ai pas suivi ta solution, elle m'a permi de trouver la mienne ! :we: