Représentation irréductible unitaire d'un groupe topologique

[dhahri]

Bonjour,
Quelqu'un peut-il m'expliquer ce qui suit:

Let G denote a topological group and , the so called dual of G, denote the set of all equivalence classes of unitary irreductible representations of G.

C'est quoi en fait ? Malgré qu'on me donne des exemples je n'arrive pas à comprendre ce que signifie ? et il est composé de quoi?
Les exemples donnés:
Si on a
Si cercle unité on a
Merci bien davantage pour l'aide

[mathelot]

Bonjour,

La question est trop technique pour le niveau moyen de ce forum (yos , connais tu la représentation linéaire des groupes finis de Serre ?).
Je te conseille de poser la question sur le forum:
les-mathématiques. net , c'est à dire, chez nos voisins du dessus. :hum:

cordialement,

[abcd22]

Bonsoir,
Pour les définitions en googlisant j´ai trouvé ça pour la définition des représentations unitaires d´un groupe topologique : « Une représentation unitaire d’un groupe topologique est un couple formé d’un espace de Hilbert et d’un morphisme de groupe continu , étant l’ensemble des endomorphismes unitaires de .»
D´une manière générale, une représentation d´un groupe G est un couple où V est un espace vectoriel et un morphisme de groupes de dans (ça revient à munir d´une structure de -module), quand il y a des hypothèses en plus sur G ou sur la représentation ça rajoute des hypothèses « logiques » dans la définition : là G est un groupe topologique donc on ajoute la continuité dans la définition du morphisme (et il faut prendre un espace vectoriel topologique pour V pour avoir une topologie sur GL(V)), et on veut un truc unitaire donc on prend un espace où il y a des morphismes unitaires à l´arrivée.
Une représentation irréductible d´un groupe est un couple tel que les seuls sous-espaces vectoriels de stables par l´action de sont {0} et , ça doit marcher aussi avec les représentations unitaires de groupes topologiques.
Si on a deux représentations d´un groupe (quelconque) et , on appelle morphisme entre ces représentations une application linéaire telle que pour tout dans , (ça revient à avoir un diagramme commutatif mais j´ai pas envie de chercher la syntaxe pour tracer les diagrammes en LaTeX), les deux représentations sont équivalentes s´il existe un morphisme de représentations qui est un isomorphisme entre U et V, c´est une relation d´équivalence. Pour définir les morphismes et isomorphismes de représentations unitaires de groupes topologiques je pense qu´il faut (et il suffit ?) rajouter l´hypothèse T continue.
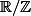
Sinon je remarque que pour tes exemples c´est la même chose que les caractères unitaires qu´on trouve, c´est logique car un caractère est juste une représentation de dimension 1 (sur )(et l´ensemble des caractères unitaires d´un groupe topologique est souvent aussi noté ), donc il suffirait de montrer que les représentations unitaires irréductibles de et sont forcément de dimension 1 sur (en dimension finie c´est pas très dur de montrer qu´il y a un vecteur propre commun, mais si V est de dimension infinie je sais pas) puis d´utiliser le résultat sur les caractères (qui est pas complètement trivial non plus...).
Enfin en résumé si tu as vraiment besoin de comprendre ça tu devrais chercher un livre qui en parle pour avoir un exposé complet avec des démonstrations (mais comme j´y connais pas grand chose j´ai pas de livre à te conseiller).