Bonjour, j'ai fait un exercice mais je ne suis pas completement sûr de ma solution. Est-ce quelqu'un pourrait m'aider? Merci.
Voilà l'exercice:
Soit

une relation sur un ensemble

, de graphe

. On a

Soir

la première projection de

sur

et
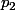
la seconde projection de

sur

. Soit

la restriction de la première projection et

la restriction de la seconde projection à

. On a
:=a)
et
:=a')
Quelle propriété sur l'image de

et

correspond à la reflexivité de

, l'antisymetrie de

et la transitivité de

?
1) pour la reflexivité:
Nous avons
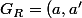; aRa')
. la reflexivité est définie par
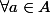
on a

. Donc ce la veut dire que la diagonale

est dans le graphe

, donc que
\in G_R)
.
Ainsi on a (avec la diagonale)
)
et
)
ainsi

est une bijection de

Pour l'antisymetrie : on a
 \in G)
et
\in G => a=a')
, ainsi nous avons

donc l'image réciproque de p1 inter l'image reciproque de p2 sont dans la diagonale (comment ecrit-on cela en latex?)
Pour la transitivité nous avons
 \in G)
et
 \in G)
=>
 \in G)
, c'est à dire que l'image reciproque de p1 pour l'ensemble des

inter l'image reciproque de p2 pour les
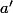
et incluse dans l'image reciproque de p1 pour les

.
Est-ce que quelqu'un pourrait m'aider à finir l'exercice ? Merci d'avance.
