Relations d'ordre

[Victhemath]

Bonjour, je suis entrain de relire mon cours de math sur les relations binaires et je tombe sur les relations d'ordre total et partiel.

On m'indique que une relation d'ordre est totale si:

quelque soient (a,b)E A², a R b ou b R a .

On me dit ensuite que la divisibilité n'est pas une relation d'ordre total mais l'inverse, c'est à dire un ordre partiel. idem pour l'inclusion sur P(E) avec |E|> ou égal à 2.

Quelqu'un peut-il me donner un exemple pour les deux cas, je voie pas très bien ce que signifie le "ou" de la définition pour l'ordre total.

Merci d'avance à vous tous !

[mr_pyer]

La relation d'ordre totale la plus simple, tout le monde la connaît c'est celle là (sur , , etc.)
Si tu prends 2 nombres, au hasard 23 et 76, on a . Maintenant si tes nombres sont a et b tu auras ou bien ou bien ...

[Ben314]

La divisibilité sur N n'est pas totale car, si tu prend a=2 et b=3 tu n'a ni a|b, ni b|a.

L'inclusion sur P(E) où E={1,2} n'est pas totale car, si tu prend A={1} et B={2} tu n'a ni A inclus dans B, ni B inclus dans A.

Par contre, la relation sur R est totale : si tu prend deux réels quelconques, on a forcément 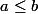ou 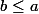(et on a les deux ssi a=b : c'est normal, c'est l'antisymétrie de la relation)

[Victhemath]

Merci Ben, tes explications sont vraiment biens !
J'ai cependant une dernière question :

Une relation est totale si a R b ou b R a. Si la relation est l'ordre stricte "<".

On a pour a=2 et b=3 :
2<3 ou 3<2. Comme on a seulement 2<3, peut-on considérer que la relation "<" comme une relation d'ordre total ?

Ma question se porte en définitive sur la signification du "ou" de la définition.

[Ben314]

Normalement, avant de se poser la question de savoir si elle est "totale" ou pas, on commence par regarder si la relation est (ou n'est pas) une relation d'ordre.
Si ce n'est pas une relation d'ordre (par exemple 0 ou y>0), alors le point (1,1) est bien dans A.

Aprés, concernant stricto senso la question que tu pose, la relation < (strictement inférieure) n'est pas une relation d'ordre et ne vérifie pas non plus la propriété "être totale" vu que, si a=b, on n'a ni a<b, ni b<a.

[Victhemath]

Normalement, avant de se poser la question de savoir si elle est "totale" ou pas, on commence par regarder si la relation est (ou n'est pas) une relation d'ordre.
Si ce n'est pas une relation d'ordre (par exemple 0 ou y>0), alors le point (1,1) est bien dans A.

Aprés, concernant stricto senso la question que tu pose, la relation < (strictement inférieure) n'est pas une relation d'ordre et ne vérifie pas non plus la propriété "être totale" vu que, si a=b, on n'a ni a<b, ni b<a.

Rien à dire, tout s'éclaire et encore merci !