Bonjour.
a, b, c sont les racines de X^3 - X - 1, je n'arrive pas à montrer que pour p premier, alors a^p + b^p + c^p est un multiple de p.
Comme a+b+c = 0, j'ai pensé calculer (a+b+c)^p = 0 = a^p+b^p+c^p + p x (....) mais je n'arrive pas à conclure.
Auriez-vous une idée? Merci.
[ désolé, faute de frappe pour le polynôme, j'ai corrigé]
Relation racine
11 messages
- Page 1 sur 1
Re: relation racine
Bonjour,
eh bien c'est fini : ça veux dire que a^p+b^p+c^p = -p x (...) c'est donc bien divisible par p.
Où alors tu regarde la relation modulo p ça donne directement a^p+b^p+c^p=0 modulo p.
eh bien c'est fini : ça veux dire que a^p+b^p+c^p = -p x (...) c'est donc bien divisible par p.
Où alors tu regarde la relation modulo p ça donne directement a^p+b^p+c^p=0 modulo p.
Re: relation racine
Merci de répondre,
dans la parenthèse, je ne sais pas si c'est un entier!!!
a, b, c ne sont pas des entiers, on peut regarder modulo p???
dans la parenthèse, je ne sais pas si c'est un entier!!!
a, b, c ne sont pas des entiers, on peut regarder modulo p???
Re: relation racine
Oui c'est vrai je n'avais pas fait attention à ça
bah du coup pour répondre il faut savoir dans quoi tu travailles ?
autrement dit où vivent les coefficients de ton polynôme ?
bah du coup pour répondre il faut savoir dans quoi tu travailles ?
autrement dit où vivent les coefficients de ton polynôme ?
Re: relation racine
Hello,
Je pense que ta méthode aboutit: si on développe (a + b + c)^p avec le multinome de Newton, tu trouves que tous les coefficients multinomiaux sont divisibles par p. Cela ne marche que pour p premier (après avoir regardé par exemple (a + b + c)^10 l'argument ne tient pas).
Ensuite, on regarde si les machins p(...) entre parenthèse sont des entiers.
A chaque fois que tu vois un produit "abc" tu peux le remplacer par -1 et il faut s'arranger pour organiser les termes du développement en fonction de (ab + bc + ac), (abc) et (a + b + c) que l'on connait en fonction des coefficients de X^3 -X-1 et qui sont des entiers.
Je ne saurais pas l'écrire proprement par contre ! Et toute la difficulté réside là
Je pense que ta méthode aboutit: si on développe (a + b + c)^p avec le multinome de Newton, tu trouves que tous les coefficients multinomiaux sont divisibles par p. Cela ne marche que pour p premier (après avoir regardé par exemple (a + b + c)^10 l'argument ne tient pas).
Ensuite, on regarde si les machins p(...) entre parenthèse sont des entiers.
A chaque fois que tu vois un produit "abc" tu peux le remplacer par -1 et il faut s'arranger pour organiser les termes du développement en fonction de (ab + bc + ac), (abc) et (a + b + c) que l'on connait en fonction des coefficients de X^3 -X-1 et qui sont des entiers.
Je ne saurais pas l'écrire proprement par contre ! Et toute la difficulté réside là

Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: relation racine
Salut Lostounet, je suis au même point que toi!! Donc bloqué également! Il doit y avoir une astuce! Dans le corrigé, le prof utilise, tranquille Fermat, est-ce possible sachant la nature de a,b,c?
[ pour infos, a^n+b^n+c^n est un entier pour tout n et parmi a,b et c il y a un réel et deux complexes conjugués]
Le théorème à montrer est: p premier implique a^p+b^p+c^p est un multiple de p
et étude de la réciproque ( en défaut pour n=217 441 )
[ pour infos, a^n+b^n+c^n est un entier pour tout n et parmi a,b et c il y a un réel et deux complexes conjugués]
Le théorème à montrer est: p premier implique a^p+b^p+c^p est un multiple de p
et étude de la réciproque ( en défaut pour n=217 441 )
Re: relation racine
Ah carrément il fallait aller jusqu'à 217 441 pour trouver ce contre-exemple?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: relation racine
Si 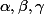 sont les racines distinctes (réelles ou complexes) de
sont les racines distinctes (réelles ou complexes) de \!=\!X^3\!-\!a X^2\!-\!b X\!-\!c) où
où  sont entiers et que, pour tout
sont entiers et que, pour tout 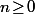 on pose
on pose 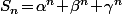 alors :
alors :
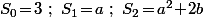 et, pour tout
et, pour tout 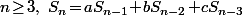 .
.
Ça montre que, pour tout ,
,  est entier et qu'on peut considérer sa classe
est entier et qu'on peut considérer sa classe 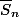 dans
dans 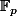 .
.
Vu que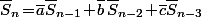 , la suite
, la suite _{n\geq 0}) est combinaison linéaire des suites
est combinaison linéaire des suites _{n\geq 0},\ (\overline{\beta}^n)_{n\geq 0},\ (\overline{\gamma}^n)_{n\geq 0}) où
où 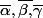 sont les racines (1) de
sont les racines (1) de \!=\!X^3\!-\!\overline{a} X^2\!-\!\overline{b} X\!-\!\overline{c}) de
de 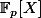 .
.
Ces racines ne sont pas forcément dans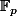 , mais éventuellement dans une extension de
, mais éventuellement dans une extension de 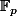 (2)
(2)
Vu les valeurs initiales de la suite, on a donc forcément et cela prouve que
et cela prouve que 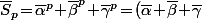^p\!=\!\overline{a}^p\!=\!\overline{a}) car
car 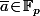
C'est à dire que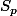 est congru à
est congru à  modulo
modulo  .
.
(1) Distinctes car vu que P est a racines distinctes, on a pgcd(P,P')=1 dans Z[X] et, via Bézout, on a aussi\!=\!1) dans
dans 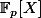 .
.
(2) Ce qui signifie en particulier qu'on a pas forcément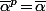 vu que cette relation caractérise les éléments de
vu que cette relation caractérise les éléments de 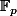 parmi ceux des extensions de
parmi ceux des extensions de 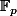 (donc si ton prof. a utilisé un truc qui ressemble à ça, ben c'est faux...)
(donc si ton prof. a utilisé un truc qui ressemble à ça, ben c'est faux...)
Ça montre que, pour tout
Vu que
Ces racines ne sont pas forcément dans
Vu les valeurs initiales de la suite, on a donc forcément
C'est à dire que
(1) Distinctes car vu que P est a racines distinctes, on a pgcd(P,P')=1 dans Z[X] et, via Bézout, on a aussi
(2) Ce qui signifie en particulier qu'on a pas forcément
Modifié en dernier par Ben314 le 29 Mar 2016, 23:12, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: relation racine
La suite (un) = (3, a+b+c, a²+b²+c², ...) est une suite récurrente (un) qui vérifie u(n+3) = u(n+1) + un, donc c'est une suite d'entiers.
Ceci est tout autant vrai quand tu prends a,b,c dans une extension de Q, que quand tu prends a,b,c dans une extension de Fp.
Si tu appelles ap,bp,cp les racines de ton polynôme mod p, alors
un mod p = ap^n + bp^n + cp^n
puisque ce sont 2 suites d'éléments de Fp qui vérifient la même équation récurrente et qui démarrent pareil.
ou alors parceque ap^n + bp^n + cp^n est une expression polynômiale en (a+b+c),(ab+bc+ac) et (abc) et que passer au modulo avant ou après revient au même
Comme x -> x^p est un automorphisme de la cloture algébrique de Fp qui permute les 3 racines ap, bp, cp, on a donc ap^p + bp^p + cp^p = ap + bp + cp = 0
Et donc up mod p = 0
(mais attention ça ne veut pas dire que un mod p est (p-1)-périodique, par exemple u(p+1) mod p peut être ab+ac+bc ou a²+2bc ou a²+b²+c² selon la manière dont le polynôme se factorise)
Ceci est tout autant vrai quand tu prends a,b,c dans une extension de Q, que quand tu prends a,b,c dans une extension de Fp.
Si tu appelles ap,bp,cp les racines de ton polynôme mod p, alors
un mod p = ap^n + bp^n + cp^n
puisque ce sont 2 suites d'éléments de Fp qui vérifient la même équation récurrente et qui démarrent pareil.
ou alors parceque ap^n + bp^n + cp^n est une expression polynômiale en (a+b+c),(ab+bc+ac) et (abc) et que passer au modulo avant ou après revient au même
Comme x -> x^p est un automorphisme de la cloture algébrique de Fp qui permute les 3 racines ap, bp, cp, on a donc ap^p + bp^p + cp^p = ap + bp + cp = 0
Et donc up mod p = 0
(mais attention ça ne veut pas dire que un mod p est (p-1)-périodique, par exemple u(p+1) mod p peut être ab+ac+bc ou a²+2bc ou a²+b²+c² selon la manière dont le polynôme se factorise)
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
