Relation fonctionnelle

[kazeriahm]

Hello

une telle fonction f est définie à une constante près (si f vérifie l'équation, f+k aussi, avec k constante)

tu peux choisir par exemple f(0)=0

regarde ce qui se passe pour f(n), avec n entier

[Doraki]

La relation indique que la fonction dépend de manière unique de sa valeur sur un intervalle de longueur 1.

Par exemple, choisis ce que tu veux sur [0;1] avec f(0)=f(1), complète avec la relation et tu obtiens une fonction continue qui vérifie la relation.

[ffpower]

tu peux en trouver une sous la forme A*cos(x)+B*sin(x) (faut resoudre un systeme en A,B..)

[ffpower]

regardons plutot le probleme ainsi:pour T fixé(disons T/2pi irrationnel),et g 2*pi periodique.On cheche f 2*pi periodique telle que f(x+T)-f(x)=g(x)(on peut facilement ramener ton enoncé a celui la).Dej,l integrale de g sur [0,2*pi] doit etre nulle pour que ce soit possible,si c est le cas,on regarde les coeff de fourier:on obtient la relation pour p different de 0 .Ainsi l equation determine les coefficients de f(a part le coeff constant).Il y a donc au plus une solution a une constante pres.Pour qu il y ait reelement une solution,il faut pouvoir définir une fonction dont les coeff de Fourier sont donnés par la relation ci dessus.Si on note ,et disons 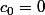,on peut définir si est sommable.C'est pas toujours le cas,mais voila un cas ou ca marche:

-il faut que T/(2*pi) soit diophantien,c est a dire mal approché par les rationnels.Plus précisément,il existe k et c strictement positifs tels que pour tout p non nul, (c est pas la vraie definition de diophantien, mais c est équivalent..).En tout cas presque tout reel est diophantien,et meme plus:presque tout nombre vérifie l inégalité précédente avec k=2

-il faut que g soit suffisament reguliere,plus précisément,qu elle soit au moins

La 2eme hypothese entraine que est bornée,et grace a la 1ere hypothese on en déduit que est bornée,et donc que (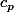 est sommable,et qu on peut donc résoudre l équation.Ca ne résous pas tous les cas,mais une solution totalement exhaustive est a ma connaissance impossible a fournir.En tout cas on obtient ainsi que si g est au moins et d integrale nulle, l equation admet une solution pour presque tout T.

[ffpower]

tu peux toujours poster,je pourrais jeter un coup d oeil si c est pas trop long(en tout cas si tes fonctions g restent des poly trigo,ca pose a priori pas de probleme de trouver f..