Bonjour, j'aurai besoin d'aide pour montrer que les relations suivantes sont des relations d'équivalence.
Soit

un ensemble non vide. Montrer que les relations suivantes définies sur
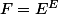
sont des relations d'équivalence :
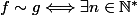
tel que
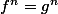
;
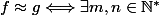
tel que
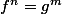
;
=g(E))
.
Voici ce que j'ai d'ores et déjà fait pour le premier :
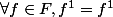
donc il existe bien un entier
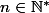
tel que
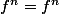
, d'où
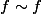
.
Par conséuqent,
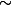
est réflexive.
Soient
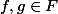
.
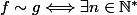
tel que
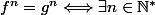
tel que
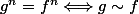
.
Donc
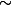
est symétrique.
Par contre, la transitivité me pose quelques problèmes :
Soient
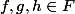
.
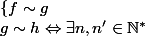
tels que
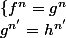
, et là je ne vois pas comment poursuivre.
J'ai pensé au ppcm(n,n'), si n divise n' ... mais je ne parvient pas à poursuivre.
Merci d'avance pour votre aide :+++:
