Relation binaire et réciproque

[baptistou]

Bonjour je rencontre un problème de réciprocité
a=>b a pour réciproque b=>a
Soit la relation R
Exemple R est la relation aimer
aRb a aime b sa réciproque semble être b est aimé par a
Par contre j ai le problème suivant
xRy <=> x+ y est pair
Comment énoncer sa réciproque je ne vois pas d' implication
Merci d' avance.
Profitant de vos connaissances le graphe de R et le graphe de R-1
Sont ils symétrique par rapport a la première bissectrice
Encore merci

[Sa Majesté]

Salut
La réciproque de R (xRy <=> x+y est pair) n'est-elle pas R elle-même ?

[barbu23]

xRy <=> x+ y est pair <=> y+ x est pair <=> yRx
:happy3:

[Ben314]

Bon, je comprend (une fois de plus) pas bien la question...
En ce qui me concerne (mais je suis passablement inculte), le mot "réciproque" n'est parfaitement clair que dans le cas de la réciproque d'une implication ce qui coorespond bien à ce que tu dit au début.
Sauf qu'ensuite, tu parle de la "réciproque" d'une relation R... sans en donner la définitions donc, forcément, comme tout concept qui n'est pas défini et ben c'est pas clair ce que ça veut dire...

Le truc qui parraitrait assez logique, vu le cas de l'implication, c'est, lorsque l'on a une relation R de définir la relation réciproque de R comme la relation R' définie par : aR'b lorsque bRa.
Si c'est bien à cette définition que tu pensait alors, par exemple, la réciproque de la relation , celle de la relation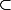 (inclus) est (contient)...
La réciproque de la relation "a aime b" est "b aime a" et celle de "x+y pair" est "y+x pair" qui dit la même chose (plus généralement, toute relation symétrique dit la même chose que sa "réciproque")
Mais je le redit : je ne crois pas que le vocable "relation réciproque" soit suffisement répendu pour que l'on puisse en parler sans en donner la définition.

Concernant ton problème de graphe, de R-1, je comprend pas non plus :
Vu le contexte, R est une relation. '1' est un entier, un réel, un complexe, à la rigueur une fonction (constante) ou une matrice (identité) et, dans aucun de ces cas, je ne comprend comment on peut retrancher '1' à une relation (d'ailleurs, je vois pas non plus quel sens donner à la somme de deux relations...)

Par contre, sur le graphe de R, là je comprend :we:
Si R est une relation sur ExE alors la relation R est symétrique si et seulement si le graphe de R est symétrique "par rapport à la première bissectrice" : c'est d'ailleurs la définition d'une "relation symétrique"

[ffpower]

A mon avis R-1=R^{-1}= réciproque de R ( telle que tu l'as définie)
Donc oui, les graphes de R et R^{-1} sont symétrique par rapport à la 1ere bissectrice ( enfin, si on parle bien de relations sur l'ensemble des réels )

[Ben314]

A mon avis R-1=R^{-1}= réciproque de R ( telle que tu l'as définie)

C'est effectivement... plus que probable...

[baptistou]

Merci pour les réponses mais difficile de définir une exactitude totale.
Dans la définition de R que je rappelle xRy<=> x+ y est pair j ai cherché
Une implication. Pensant que x+y => pair pour moi la réciproque devient
Pair => y+ x pourquoi mon raisonnement semble erroné

[Ben314]

... Pensant que x+y => pair ...

Un petit "rappel" : de la même façon que, quand on écrit le symbole // (parallèle) on met des deux cotés des droites (et pas des réels...), lorsque l'on utilise le symbole =>, on met des deux coté des affirmations (des truc qui peuvent être vrai ou faux).
Or, il ne me semble pas que "x+y" soit une affirmation, ni que "pair" en soit une (ça manque légèrement de verbe...)
Donc un qu'un truc comme "x+y => pair", ça à a peu prés autant de sens que par exemple "Pi est parallèle à racine(2)" si tu vois ce que je veut dire... :mur: