Reimann ...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 14 Avr 2007, 00:46
par rifly01 » 14 Avr 2007, 00:46
Bonjour,
J'ai une petite difficulté à répondre à cette question :
!}{n!}}\Big))
Donnez-moi des petites indications, je me chergerai du reste.
Merci d'avance.
-
serge75
- Membre Relatif
- Messages: 432
- Enregistré le: 05 Avr 2006, 22:31
-
 par serge75 » 14 Avr 2007, 02:06
par serge75 » 14 Avr 2007, 02:06
A priori, et sans l'avoir fait, j'aurais envie de t'inviter à prendre le logarithme de ton expression pour voir apparaître une somme de Riemann, comme le titre de ton post l'indique.
Serge
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 14 Avr 2007, 04:39
par rifly01 » 14 Avr 2007, 04:39
A vos ordres chef,
!}{n!}}\Big]=-lnn+\frac{1}{n}ln\Big(\frac{(2n)!}{n!}\Big))
-
serge75
- Membre Relatif
- Messages: 432
- Enregistré le: 05 Avr 2006, 22:31
-
 par serge75 » 14 Avr 2007, 07:14
par serge75 » 14 Avr 2007, 07:14
Continue... Une factorielle est un produit, n'oublie pas...
Puis essaie d'arriver à écrire le tout sous la forme (1/n) fois une somme.
Serge
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 14 Avr 2007, 07:43
par fahr451 » 14 Avr 2007, 07:43
bonjour
4/e est la limite
-
serge75
- Membre Relatif
- Messages: 432
- Enregistré le: 05 Avr 2006, 22:31
-
 par serge75 » 14 Avr 2007, 11:39
par serge75 » 14 Avr 2007, 11:39
Autre indication : pour tout nombre a, on a :

-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 14 Avr 2007, 15:17
par rifly01 » 14 Avr 2007, 15:17
Re -
On remarque que :
!}{n!}=(n+1)(n+2) ... (2n))
Et donc
!}{n!}}=\frac{1}{n}\sqrt[n]{(n+1)(n+2)...(2n)}=\sqrt[n]{\frac{n+1}{n}\frac{n+2}{n}...\frac{2n}{n}} =\sqrt[n]{\prod_{k=1}^{n}\Big(1+\frac{k}{n}\Big)}=a_n)
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 14 Avr 2007, 15:19
par fahr451 » 14 Avr 2007, 15:19
fais donc rentrer le 1/n sous la racine et prends le log (bis)
-
serge75
- Membre Relatif
- Messages: 432
- Enregistré le: 05 Avr 2006, 22:31
-
 par serge75 » 14 Avr 2007, 15:24
par serge75 » 14 Avr 2007, 15:24
du log, du log, du log !
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 14 Avr 2007, 15:27
par rifly01 » 14 Avr 2007, 15:27
Lol,
merci les gas !!!

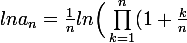\Big)= \frac{1}{n}\sum_{k=1}^{n}ln\Big(1+\frac{k}{n}\Big)\equiv \int_{0}^{1}ln(1+x)dx=..=2ln2-1 => a_n=\frac{4}{e})
Enocre un merci,
-
serge75
- Membre Relatif
- Messages: 432
- Enregistré le: 05 Avr 2006, 22:31
-
 par serge75 » 14 Avr 2007, 15:30
par serge75 » 14 Avr 2007, 15:30
je crois qu'on peut dire que le plus dur est fait...
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 14 Avr 2007, 15:34
par rifly01 » 14 Avr 2007, 15:34
en effet, (dirait Telc) ... lol
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 95 invités