Regularite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 04 Nov 2015, 11:13
par adamNIDO » 04 Nov 2015, 11:13
Bonjour,
dans l'exemple suivante ca laire que redacteur a pris
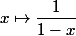
comme une fonction de classe
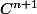
sur
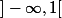
et ne pas dans
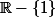
pouvez vous m'expliquer pourquoi

merci d'avance
-
Robot
 par Robot » 04 Nov 2015, 11:18
par Robot » 04 Nov 2015, 11:18
Qui peut le plus peut le moins. Et comme l'auteur s'intéresse au développement limité à l'origine, l'intervalle
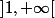
est vraiment superflu.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 04 Nov 2015, 11:31
par adamNIDO » 04 Nov 2015, 11:31
Robot a écrit:Qui peut le plus peut le moins. Et comme l'auteur s'intéresse au développement limité à l'origine, l'intervalle
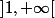
est vraiment superflu.
donc si j'ai bien compris il me suffit de prendre le voisinage de

:
)
c'est largement suffisante
=]-\epsilon,+\epsilon [)
-
Robot
 par Robot » 04 Nov 2015, 11:34
par Robot » 04 Nov 2015, 11:34
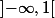
est un joli voisinage de 0. Il ne te plaît pas ?
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 04 Nov 2015, 11:36
par adamNIDO » 04 Nov 2015, 11:36
Robot a écrit: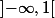
est un joli voisinage de 0. Il ne te plaît pas ?
pouvez vous m'explique pourquoi s'il vous plait et est ce que on peut aussi prendre
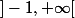
je me demande pourquoi exactement il a pris
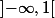
et pas autre voisinage de 0 ou bien c'est une question de choix
merci d'avance
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 04 Nov 2015, 12:56
par MouLou » 04 Nov 2015, 12:56
La fonction n est pas définie en 1. Il prend juste le plus grand ouvert qui contient 0, cava pas plus loin je pense
-
Robot
 par Robot » 04 Nov 2015, 12:58
par Robot » 04 Nov 2015, 12:58
adamNIDO a écrit:pouvez vous m'explique pourquoi s'il vous plait et est ce que on peut aussi prendre
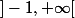
je me demande pourquoi exactement il a pris
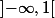
et pas autre voisinage de 0 ou bien c'est une question de choix
merci d'avance
Franchement, je ne comprends pas les questions que tu te poses. Pourquoi ne pas prendre
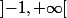
? Ben tout bêtement parce que la fonction n'est pas définie en 1 !
Pourquoi exactement il a pris
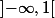
? Parce que la fonction est visiblement définie et de classe

sur cet intervalle, qui est un voisinage de 0.
Le choix de ce voisinage de 0 n'a aucune importance ! Tu te fais des noeuds dans la tête pour des choses qui n'en valent pas la tête.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 04 Nov 2015, 13:20
par adamNIDO » 04 Nov 2015, 13:20
MouLou a écrit:La fonction n est pas définie en 1. Il prend juste le plus grand ouvert qui contient 0, cava pas plus loin je pense
merci beaucoup
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 04 Nov 2015, 13:22
par adamNIDO » 04 Nov 2015, 13:22
Robot a écrit:Franchement, je ne comprends pas les questions que tu te poses. Pourquoi ne pas prendre
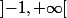
? Ben tout bêtement parce que la fonction n'est pas définie en 1 !
Pourquoi exactement il a pris
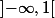
? Parce que la fonction est visiblement définie et de classe

sur cet intervalle, qui est un voisinage de 0.
Le choix de ce voisinage de 0 n'a aucune importance ! Tu te fais des noeuds dans la tête pour des choses qui n'en valent pas la tête.
Merci pour votre explication concernant les noeuds j'ai essayé d'apprendre les choses en détailles.
s'il vous plait pourquoi la puissance 4 disparaître dans la dernière terme a droite

-
Robot
 par Robot » 04 Nov 2015, 13:50
par Robot » 04 Nov 2015, 13:50
adamNIDO a écrit:s'il vous plait pourquoi la puissance 4 disparaître dans la dernière terme a droite
Parce qu'on développe
)^4)
.
Un exemple simple de développement :
)^4= 1+4x+o(x))
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 04 Nov 2015, 14:15
par adamNIDO » 04 Nov 2015, 14:15
Robot a écrit:Parce qu'on développe
)^4)
.
Un exemple simple de développement :
)^4= 1+4x+o(x))
c'est comme on a utilise
^a = 1 + ax + \frac{a(a-1)}{2!}x^2 + \frac{a(a-1)(a-2)}{3!}x^3 + \cdots + \frac{a(a-1)(a-2)...(a-(n-1))}{n!}x^n + o(x^n))
-
Robot
 par Robot » 04 Nov 2015, 14:43
par Robot » 04 Nov 2015, 14:43
Oui, mais il y a aussi un o(x) dans ce que j'ai élevé à la puissance 4. Et quand on développe, tout ce qui dépasse la puissance 1 est englouti dans le o(x).
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 04 Nov 2015, 15:35
par adamNIDO » 04 Nov 2015, 15:35
Robot a écrit:Oui, mais il y a aussi un o(x) dans ce que j'ai élevé à la puissance 4. Et quand on développe, tout ce qui dépasse la puissance 1 est englouti dans le o(x).
si j'ai bien compris
)^4= 1+4x+o(x))
)^4&= 1+4x+o(x)\\<br />\text{ posant x+o(x)=y }& \\<br />(1+x+o(x))^4&= 1+4Y+o(Y)\\<br />(1+x+o(x))^4&= 1+4(x+o(x))+o(x+o(x))\\<br />(1+x+o(x))^4&= 1+4x+4o(x))+o(x)+o(o(x))\\<br />(1+x+o(x))^4&= 1+4x+o(4x))+o(x)+o(x)\\<br />(1+x+o(x))^4&= 1+4x+o(x))\\<br />\end{align})
n'est ce pas mais si je voudrais travaille avec le cas de l'exemple en question
)^4&=(1+\ldots+o(x^{n-1}))\\<br />\text{ posant y=\ldots+o(x^{n-1}) }& \\<br />(1+\ldots+o(x^{n-1}))^4&= 1+4Y+o(Y)\\<br />(1+\ldots+o(x^{n-1}))^4&= 1+4(\ldots+o(x^{n-1}))+o(\ldots+o(x^{n-1}) )\\<br />(1+\ldots+o(x^{n-1}))^4&= 1+(4\times \ldots+4\times o(x^{n-1}))+o(\ldots )+o(o(x^{n-1})) )\\<br />(1+\ldots+o(x^{n-1}))^4&= 1+ \ldots+ o(x^{n-1})+o(\ldots )+o(x^{n-1}) \\<br />(1+\ldots+o(x^{n-1}))^4&= 1+ \ldots+o(\ldots )+o(x^{n-1})+ o(x^{n-1}) \\<br />(1+\ldots+o(x^{n-1}))^4&= 1+ \ldots+o(\ldots )+o(x^{n-1}) \\<br />\end{align})
 ce qui est entre petit o(\ldots ) leurs degre est plus petit que o(x^{n-1}) } \\<br />(1+\ldots+o(x^{n-1}))^4= 1+ \ldots+o(\ldots )+o(x^{n-1}) \\)
est ce que mon raisonnement est correcte
-
Robot
 par Robot » 04 Nov 2015, 17:13
par Robot » 04 Nov 2015, 17:13
Nan. C'est un peu du n'importe quoi avec les points de suspension.
Je reprends un exemple
)^4= 1+4x+ 10x^2 +o(x^2))
Je te laisse y réfléchir. Commence par développer
^4)
.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 04 Nov 2015, 17:25
par adamNIDO » 04 Nov 2015, 17:25
Robot a écrit:Nan. C'est un peu du n'importe quoi avec les points de suspension.
Je reprends un exemple
)^4= 1+4x+ 10x^2 +o(x^2))
Je te laisse y réfléchir. Commence par développer
^4)
.
je vais refaire votre exemple mais est ce qu'on a en generale:
+o(x^{n-1}))^{\alpha}=(p(x)+o(x^{n-1})))
avec
)
un polynome de degre

et
=1)
et
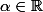
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 04 Nov 2015, 18:06
par adamNIDO » 04 Nov 2015, 18:06
voici une déclaration plus précise de ce que le papier réclame:
si
=p(x)+o(x^n))
tel que
)
est une polynôme avec
=1)
, alors:
^4 = q(x) + o(x^n))
tel que
)
est une polynôme avec
=1)
.
-
Robot
 par Robot » 04 Nov 2015, 18:20
par Robot » 04 Nov 2015, 18:20
adamNIDO a écrit:voici une déclaration plus précise de ce que le papier réclame:
si
=p(x)+o(x^n))
tel que
)
est une polynôme avec
=1)
, alors:
^4 = q(x) + o(x^n))
tel que
)
est une polynôme avec
=1)
.
Si
=p(x)+o(x^n))
où

est un polynôme de degré
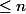
, alors
^4 = p(x)^4 + o(x^n))
, et on peut faire rentrer tous les monômes de
^4)
de degré

dans le
)
. (Les

sont au voisinage de 0).
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 04 Nov 2015, 18:24
par adamNIDO » 04 Nov 2015, 18:24
Robot a écrit:Si
=p(x)+o(x^n))
où

est un polynôme de degré
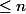
, alors
^4 = p(x)^4 + o(x^n))
, et on peut faire rentrer tous les monômes de
^4)
de degré

dans le
)
. (Les

sont au voisinage de 0).
mais comment montrer cette proposition
-
Robot
 par Robot » 04 Nov 2015, 18:44
par Robot » 04 Nov 2015, 18:44
Un petit exercice pour toi. Tu sais sans doute développer
^4)
? Et si les
)
t'effraient, tu peux les écrire sous la forme
)
avec
=0)
.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 05 Nov 2015, 09:11
par adamNIDO » 05 Nov 2015, 09:11
Robot a écrit:Un petit exercice pour toi. Tu sais sans doute développer
^4)
? Et si les
)
t'effraient, tu peux les écrire sous la forme
)
avec
=0)
.
Bonjour,
par formule de binôme on a :
^{4} &= a^{4} +4a^{3}b + 6a^{2}b^{2} + 4ab^{3} + b^{4}\\<br />(a - b)^{4} &= a^{4} + b^{4}-4a^{3}b + 6a^{2}b^{2} -4ab^{3} \\<br />\end{align})
le développement en dessus nous donne pas
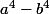
donc on je pense qu'on doit utilise :
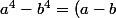(a^3 + a^2b+ab^2+b^3))
n'est ce pas ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités


et pas autre voisinage de 0 ou bien c'est une question de choix
? Ben tout bêtement parce que la fonction n'est pas définie en 1 !
? Parce que la fonction est visiblement définie et de classe
sur cet intervalle, qui est un voisinage de 0. Le choix de ce voisinage de 0 n'a aucune importance ! Tu te fais des noeuds dans la tête pour des choses qui n'en valent pas la tête.
