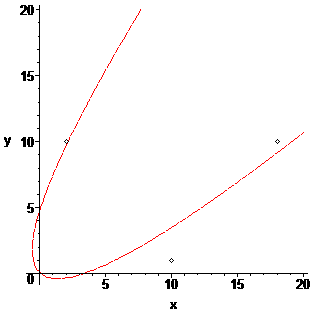
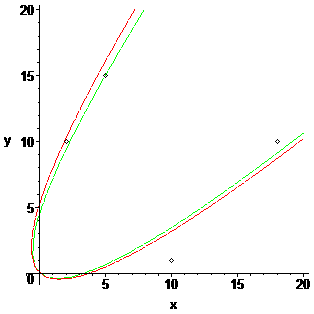
par sylvain231 » 19 Juin 2023, 17:13
par sylvain231 » 19 Juin 2023, 17:13
mes points pour tes tests sont :
[141, 242]
[123, 242]
[142, 243]
[143, 243]
[124, 243]
[124, 244]
[144, 244]
[144, 244]
[125, 244]
[126, 245]
[145, 245]
[145, 245]
[127, 245]
[128, 246]
[146, 246]
[146, 246]
[129, 247]
[147, 247]
[147, 247]
[130, 248]
[149, 248]
[131, 249]
[150, 249]
[150, 249]
[132, 250]
[133, 250]
[151, 251]
[134, 251]
[151, 251]
[135, 251]
[135, 252]
[152, 252]
[152, 252]
[136, 252]
[136, 253]
[154, 253]
[154, 253]
[138, 254]
[155, 254]
[139, 255]
[139, 255]
[156, 255]
[156, 256]
[141, 256]
[141, 256]
[158, 257]
[158, 257]
[142, 257]
[143, 258]
[159, 258]
[159, 258]
[144, 259]
[144, 259]
[145, 259]
[161, 260]
[161, 260]
[146, 260]
[146, 260]
[147, 261]
[162, 261]
[162, 261]
[162, 261]
[149, 262]
[164, 262]
[164, 263]
[149, 263]
[164, 263]
[150, 263]
[150, 263]
[166, 264]
[166, 264]
[166, 264]
[153, 265]
[153, 265]
[153, 266]
[167, 266]
[168, 266]
[154, 266]
[168, 266]
[154, 266]
[155, 267]
[155, 267]
[155, 267]
[156, 268]
[169, 268]
[169, 268]
[156, 268]
[170, 268]
[170, 268]
[157, 268]
[157, 268]
[157, 269]
[158, 269]
[158, 269]
[159, 270]
[172, 270]
[172, 270]
[159, 270]
[172, 270]
[172, 270]
[159, 270]
[160, 271]
[162, 272]
[162, 272]
[174, 272]
[174, 272]
[174, 272]
[163, 273]
[174, 273]
[175, 273]
[175, 273]
[163, 273]
[163, 273]
[164, 274]
[165, 274]
[165, 275]
[166, 275]
[167, 276]
[178, 276]
[178, 276]
[167, 276]
[178, 276]
[178, 276]
[178, 276]
[168, 276]
[178, 276]
[179, 277]
[179, 277]
[168, 277]
[179, 277]
[179, 277]
[179, 277]
[179, 277]
[179, 277]
[169, 277]
[179, 277]
[179, 277]
[179, 277]
[169, 278]
[180, 278]
[180, 278]
[180, 278]
[180, 278]
[180, 278]
[170, 278]
[180, 278]
[171, 279]
[171, 279]
[181, 279]
[181, 279]
[181, 279]
[181, 279]
[172, 279]
[181, 279]
[181, 279]
[182, 280]
[182, 280]
[182, 280]
[173, 280]
[182, 280]
[182, 280]
[182, 280]
[182, 280]
[182, 280]
[173, 280]
[182, 280]
[182, 280]
[183, 281]
[174, 281]
[183, 281]
[183, 281]
[174, 281]
[183, 281]
[183, 281]
[183, 281]
[175, 281]
[175, 282]
[176, 282]
[176, 283]
[177, 283]
[177, 283]
[185, 283]
[185, 283]
[185, 283]
[185, 284]
[186, 284]
[178, 284]
[186, 284]
[178, 284]
[179, 284]
[179, 285]
[180, 285]
[187, 285]
[187, 285]
[180, 285]
[187, 285]
[187, 285]
[180, 285]
[181, 285]
[181, 286]
[188, 286]
[188, 286]
[188, 286]
[188, 286]
[188, 287]
[189, 287]
[183, 287]
[189, 287]
[183, 287]
[184, 287]
[189, 288]
[184, 288]
[189, 288]
[184, 288]
[189, 288]
[185, 288]
[190, 288]
[190, 288]
[185, 288]
[185, 289]
[190, 289]
[185, 289]
[190, 289]
[190, 289]
[186, 289]
[190, 289]
[186, 289]
[190, 289]
[186, 289]
[190, 289]
[187, 289]
[190, 289]
[187, 289]
[191, 289]
[187, 290]
[191, 290]
[187, 290]
[191, 290]
[187, 290]
[191, 290]
[188, 290]
[191, 290]
[188, 290]
[191, 290]
[188, 290]
[191, 290]
[188, 290]
[189, 290]
[191, 290]
[189, 291]
[191, 291]
[189, 291]
[191, 291]
[189, 291]
[191, 291]
[189, 291]
[191, 291]
[191, 291]
[190, 291]
[191, 291]
[191, 291]
[190, 291]
[190, 291]
[191, 291]
[191, 291]
[190, 291]
[190, 291]
[191, 291]
[191, 291]