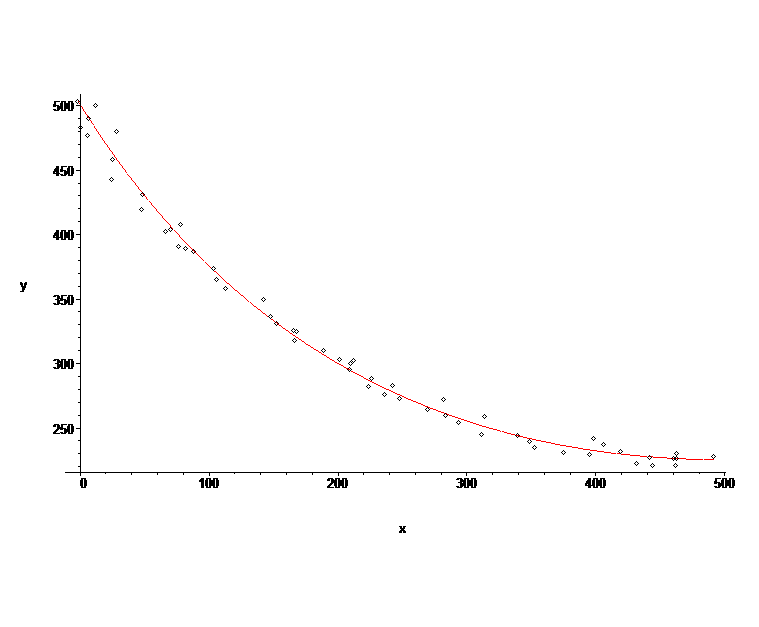
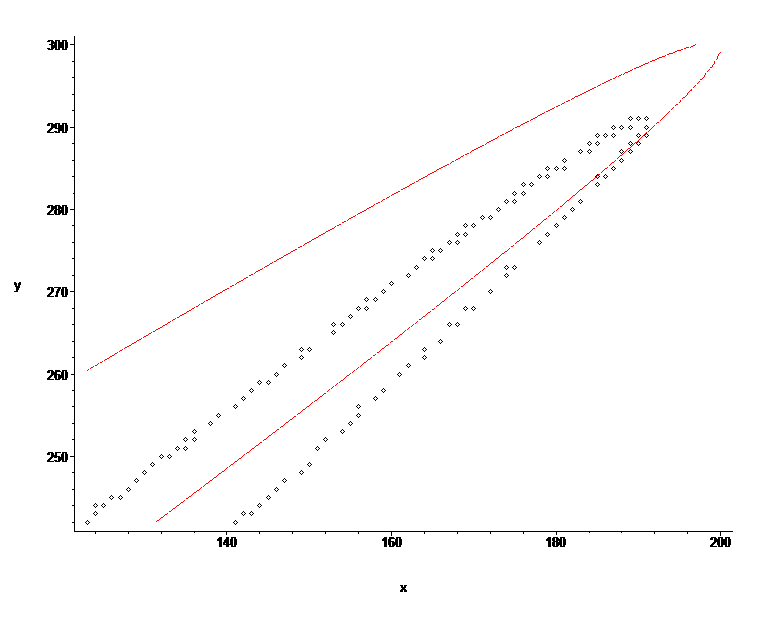
Régression parabolique non triviale

[sylvain231]

léon peux-tu nous mettre la courbe de la parabole plate pour qu'on puisse voir si le minimum est encadré par deux maxima ?

[sylvain231]

donc est-ce que lancer les deux algos, calculer l'erreur même grossière et choisir le meilleur ?

[sylvain231]

Bon, pour résumer la journée :

minimiser fonctionne pour la parabole plate, pas la serrée.

minimiser fonctionne pour la parabole serrée, pas la plate. >> moi ça ne marchait pas pour la serrée tu dois confondre avec un autre algo

[Ben314]

Dans la boucle où on cherche le min. de la fonction F dépendant de theta., si on mémorise les deux dernières valeurs trouvées F2 (il y a deux coups) et F1 (le coup précédent) plus la valeur calculée F0, alors :
1) Pour que F1 soit un minimum local, il faut évidement qu'il soit plus petit à la fois que F0 et F2.
2) Le "creux" que la courbe fait à cet endroit là peut être mesuré en calculant F0+F2-2xF1 : plus cette quantité est grande, plus le "creux" est prononcé.
Donc dans la boucle, on cherche quand-est ce que la condition 1) est vérifiée et s'il y a plusieurs points vérifiant cette condition, on prend celui donnant la plus grande valeur pour F0+F2-2F1 (en faisant gaffe à prendre comme theta celui correspondant à F1 et pas à F0).

[leon1789]

donc est-ce que lancer les deux algos, calculer l'erreur même grossière et choisir le meilleur ?

comment calcules-tu << l'erreur >> ?

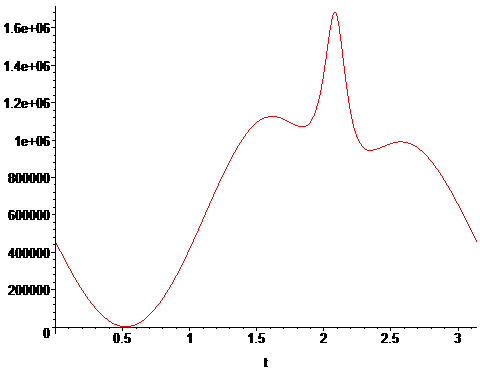
léon peux-tu nous mettre la courbe de la parabole plate pour qu'on puisse voir si le minimum est encadré par deux maxima ?

Voici le graphe de la fonction minimisant pour la plate :

[leon1789]

minimiser fonctionne pour la parabole serrée, pas la plate.

moi ça ne marchait pas pour la serrée tu dois confondre avec un autre algo

si si, on avait les mêmes valeurs toi et moi, c'était ce passage :
superieur/regression-parabolique-non-triviale-t278846-200.html#p1549170

[lyceen95]

A base de force brute, mais pas complètement brute.
On sait quels points sont sur la branche de droite et lesquels sont sur la branche de gauche.
On peut calculer la distance de chaque point au sommet. Cette distance, combinée avec la notion de droite/gauche permet de classer les points dans l'ordre, sans erreur ou quasiment.
Et on peut tracer une succession de segments, qui est une bonne approximation de la parabole.
On peut prendre 2 points de ce 'polyligne', assez éloignés du sommet, tous 2 à même distance du sommet imposé, un sur chacune des 2 branches (pas forcément des points issus du set de points initial, ça peut être des points au milieu de tel segment). Le milieu de ces 2 points nous donne une assez bonne approximation de la direction de l'axe de la parabole.
Et ces 2 points nous donnent aussi une assez bonne approximation du coefficient a.
Après, on enclenche la force brute, avec des faibles variations autour de cette direction et autour de ce coefficient a.

[leon1789]

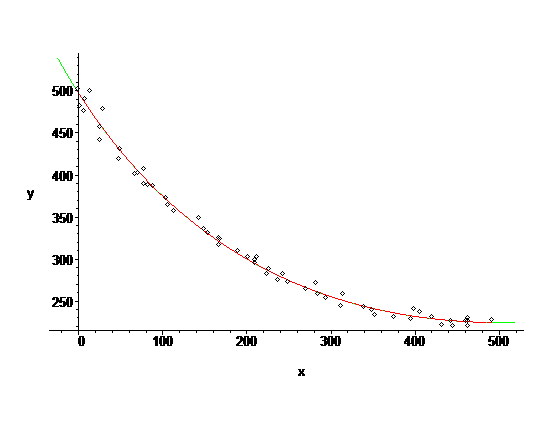
On peut prendre 2 points de ce 'polyligne', assez éloignés du sommet, tous 2 à même distance du sommet imposé, un sur chacune des 2 branches (pas forcément des points issus du set de points initial, ça peut être des points au milieu de tel segment). Le milieu de ces 2 points nous donne une assez bonne approximation de la direction de l'axe de la parabole.

Si je comprends bien ton idée, alors cela ne fonctionnera pas sur le bout de parabole plate : la direction obtenue sera plutôt orthogonale à l'axe de la parabole, dont le sommet est (200 ; 300)

[lyceen95]

Dans mon plan, je prends 2 points A et B tous les 2 à une même distance D du sommet S, un sur chaque branche de la parabole.
Puis je prends le milieu M de AB.
L'axe de la parabole passe par S et par un point proche de M.
La distance D dont je parle, c'est la distance euclidienne

Sur l'exemple que tu proposes, la direction sera globalement bonne, mais la qualité de la précision pas terrible. Comme M va être proche de S, la moindre erreur d'une unité sur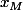 ou 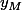va entrainer un changement de direction de 3 ou 5 degrés.

[leon1789]

Ok, cela donne une première approximation de l'angle de rotation.

[leon1789]

J'ai aussi une autre idée : calculer une conique proche des points, avec 2 contraintes imposées (je détaillerai),
puis modifier les coefficients de cette conique pour qu'elle devienne une parabole avec le sommet fixé.

[sylvain231]

lyceen95 peux-tu STP me décrire en détail l'algo que je teste STP ?
Merci

[sylvain231]

et de plus je ne pourrais pas tester la méthode de lyceen95 sur les deux exemples habituels car je ne peux pas trouver facilement les points à gauche et à droite du sommet dans ces exemples. Dans mon programme final je les connaitrais mais il n'est pas encore codé. Pour générer ces suites de points j'ai pris des équations de parabole auxquelles j'ai rajouté du bruit. Pour les tests du code de lyceen95 pourriez vous me dire comment séparer les points à gauche et à droite du sommet connaissant l'équation de la parabole en a et theta que je puisse générer des suites de points pour les tests SVP ?

[leon1789]

oups.

[sylvain231]

ah je sais comment trouver les points à gauche et à droite de la parabole, il suffit de translater tous les points de -sommet et de les tourner de -theta puis ceux qui ont un x à gauche sont ceux à gauche et ceux qui ont un x à droite sont ceux à droite est-ce bon ? (est-ce notamment theta ou - theta ?)

[leon1789]

J'indique tout de même ce à quoi j'arrive avec un peu de calcul matriciel.

Je considère la matrice M de n lignes
Je considère la matrice B de n lignes

Je précise que je pose ce système en fixant un point (~sommet) à (0,0) et en imposant que les futurs coefficients de x^2 et y^2 soit de somme 1, comme il se doit dans les paraboles que l'on cherche :


Je vais résoudre en Z par les moindres carrés l'équation M * Z = B
Pour cela, on multiplie par la transposée de M , donc tM * M * Z = tM * B

Je note N = tM * M la matrice 4x4 du système linéaire.

Exemple sur la parabole plate :


Exemple sur la parabole serrée :



On résout le système N * Z = tM * B , ce qui donne Z .
Le vecteur Z possède 4 coordonnées et on obtient une conique "proche" de la parabole cherchée :


Il va sans dire que les calculs sont instantanés.

Ensuite, on modifie la conique pour quelle devienne une parabole.
La conique peut être une ellipse ou une hyperbole, il faut en tenir compte.
Je passe les modifications (que l'on peut surement améliorer)
et j'obtiens ces résultats :

[leon1789]

Pour la parabole plate (la conique initiale est une ellipse) :

[leon1789]

Pour la parabole serrée (la conique initiale est une hyperbole)

[leon1789]

Je pense que je peux améliorer les résultats. A suivre.

[sylvain231]

pour la parabole serrée tu peux mettre le vrai sommet c'était dû à une erreur de mon bruitage de parabole qui faisait toujours -2