Reformulation d'une preuve

[Guillermo]

Bonjour à tous, voici la preuve d'un théorème donnée par mon livre, je vais commenter les deux passages en gras car je ne suis pas sûr de les comprendre, n'hésitez pas à me corriger si j'ai mal compris :
THEOREM : The set P of positive integers 1, 2, 3, . . . is unbounded above.
PROOF : Assume P is bounded above. We shall show that this leads to a contradiction. Since P is nonempty, Axiom 10 tells us that P has a least upper bound, say b. The number b-1, being less than b, cannot be an upper bound for P. Hence, there is at least one positive integer n such that n>b-1. For this n we have n+1 > b. Since n+1 is in P, this contradicts the fact that b is an upper bound for P.
AXIOM 10 : Every nonempty set S of real numbers which is bounded above has a supremum; that is, there is a real number B such that B = sup S.
Explication du 1er passage en gras : Nous savons que b > b-1, autrement dit il existe au moins un nombre entier positif (b en l'occurrence) qui est supérieur à b-1, autrement dit il existe au moins un nombre entier positif qu'on appellera n et qui est supérieur à b-1.
Explication du 2e passage en gras :
1) Puisque n est un entier positif, alors nécessairement n ∈ P, puisque P est l'ensemble des entiers positifs ;
2) Puisque P est un ensemble inductif, par définition, pour tout élément x ∈ P, le nombre x+1 ∈ P.
3) En conséquence des deux points précédents, le nombre n+1 ∈ P.

Voilà, toutefois je ne suis pas sûr de comprendre pourquoi le fait que b soit le supremum (autrement dit le least upper bound) de P impliquerait que b soit un entier positif... Une aide svp ?
Merci beaucoup !

[GaBuZoMeu]

Bonjour,
Tu t'es aperçu de ta faute de raisonnement : rien ne te permet de dire que est entier.
est par définition le plus petit majorant de . Comme , 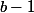n'est pas un majorant de (si c'était le cas, ne serait pas le plus petit !). Donc il existe un élément de , c.-à-d. un entier positif,, strictement plus grand que 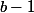. Soit un tel entier positif ... je te laisse continuer.

[Guillermo]

Ok ! En d'autres termes, comme b-1 n'est pas un majorant de P et comme un majorant (noté x) de P se définit comme x tel que y ≤ x pour tout y appartenant à P, alors nécessairement il existe au moins un y appartenant à P tel que y > x. Comme ce y appartient à P et comme P est l'ensemble des entiers positifs, alors nécessairement y est un entier positif. On notera ce y par n. Ai-je bon ? Merci encore !

[GaBuZoMeu]

Suis bien les définitions, et reste simple : pourquoi donner deux noms à la même chose ? Un entier n'est pas plus entier parce que tu l'appelles plutôt que !

[Guillermo]

Merci, effectivement le fait d'utiliser à la fois y et n alourdit mon message, je n'aurais pas du faire ça. Sinon je pense que le raisonnement est correct cela dit

[GaBuZoMeu]

Oui, puisque c'est le raisonnement correct du texte que tu as compris.