Reflexions

[guigui777]

On veut montrer qu'un automorphisme orthogonal f de E est la composée d'au plus n reflexions...n>1
on fait une récurence sur n,
si n=2
s'il existe x tq f(x)=x on regarde y € xorthogonal, et f(y)=y ou -y, donc f c'est soit l'identité soit la reflexion par rapport à vectx, je comprend ca mais je vois pas les 2 réflexions... y'en à qu'une à chaque fois...?

[B_J]

Salut ;
c'est quoi n ? dim E ?

Code: Tout sélectionner

On veut montrer qu'un automorphisme orthogonal f de E est la composée
[B][I][COLOR=Red]d'au plus[/COLOR][/I][/B] n reflexions...n>1

[aviateurpilot]

On veut montrer qu'un automorphisme orthogonal f de E est la composée d'au plus n reflexions...n>1
on fait une récurence sur n,
si n=2
s'il existe x tq f(x)=x on regarde y € xorthogonal, et f(y)=y ou -y, donc f c'est soit l'identité soit la reflexion par rapport à vectx, je comprend ca mais je vois pas les 2 réflexions... y'en à qu'une à chaque fois...?

soit S la reflexion par rapport à vect(x),
ou

[guigui777]

soit S la reflexion par rapport à vect(x),
ou

ok, après on fait l'hypothèse de rec, au rang n-1
on regarde au rang n, si il existe x tel que f(x)=x, on reregarde xortho, qui est de dimension n-1 et on applique l'hypothèse de récurrence, f restreint a xortho est donc bien la composée d'au plus n-1 reflexion, s1.....sp
pour conclure il faut dire quoi? revenir au rang n...?
Dans mon cour j'ai: s laisse stable F de dimension n-2, et on étend à vect(x)+H...
je c'est pas ce que c'est ce H l'hyperplan à vect(x)?

[yos]

Bonjour.
J'ai pas compris ta question.
Alors je reprends la preuve :
1) si il existe x non nul tel que f(x)=x, on pose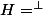 . Il faut d'abord vérifier que f laisse stable H (facile mais indispensable). Ensuite on peut appliquer l'hypothèse de récurrence à :
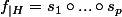, avec et 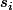réflexion de "plan" 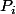(dimension n-2).
On peut noter s'_i la réflexion de E d'hyperplan . Tu peux alors vérifier que .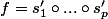

2) Ensuite il faut envisager le cas où f n'a pas de point fixe.

[aviateurpilot]

si n'a pas de point fixe.
soit
et soit la reflexion tel que
et donc a un poin fixe , et tu fait le meme resonnement sur l'automorphisme
et tu utilise le fait que si alors

[guigui777]

ok pour ca mais ma question c'est pourquoi on prend si la réflexion de plan de dimension n-2

[guigui777]

Bonjour.
J'ai pas compris ta question.
Alors je reprends la preuve :
1) si il existe x non nul tel que f(x)=x, on pose . Il faut d'abord vérifier que f laisse stable H (facile mais indispensable). Ensuite on peut appliquer l'hypothèse de récurrence à :
, avec et réflexion de "plan" (dimension n-2).
On peut noter s'_i la réflexion de E d'hyperplan . Tu peux alors vérifier que .

2) Ensuite il faut envisager le cas où f n'a pas de point fixe.

donc f est la composée d'au plus n-1 symétrie or on veux au rang n... donc au plus n symétries

[aviateurpilot]

donc f est la composée d'au plus n-1 symétrie or on veux au rang n... donc au plus n symétries

yos a dit que si il exist x tel que f(x)=x
alors f est composé de n-1 reflexion.
tu doi revoir mon raisonnement pour l'aute cas ou klk soit x, et tu va comprendre que danse ce cas f peux etre composé d'au plus n reflexion

attention: symétrie n'est pas forcement reflexion

[guigui777]

yos a dit que si il exist x tel que f(x)=x
alors f est composé de n-1 reflexion.
tu doi revoir mon raisonnement pour l'aute cas ou klk soit x, et tu va comprendre que danse ce cas f peux etre composé d'au plus n reflexion

attention: symétrie n'est pas forcement reflexion

oki jvois bien que la suite nous montre que c'est au plus n, néanmoins je n'ai toujours pas compris a quoi servais la partie sur Pi, puisque on a déjà f restreinte à H qui est une la composition d'au plus n-1 symétries?
Enfin je ne vois vraiment pas, on prend un plan Pi de dim n-2, ok et après si la réflexion de plan Pi, si je prend x, donc j'ai une symétrie par rapport à Pi, et s'i je ne vois pas trop ce que c'est la réflexion par rapport a H+vect(x), ca me donne pas f(x )?

[yos]

Une réflexion c'est une symétrie par rapport à un hyperplan. Donc quand tu appliques l'hypothèse de récurrence tu obtiens des symétries par rapport à des espaces de dimension n-2 (car (n-1)-1=n-2 non?). D'où la nécessité de fabriquer des symétries par rapport à des hyperplans.

[guigui777]

ok ca va je vois le truc merci!