Réduction de matrices

[vejitoblue]

salut

comme je vous ai précisé avant, les determinants c'est pas mon truc: en général pour calculer le polynome caracteristique j'utilise la méthode de cramer (il me semble que ça s'appelle comme ça). C'est plutot brutal et ça me dérange pas avec des matrice 3x3.



avec ma méthode on se retrouve avec la somme de determinant de 4 matrice 3x3 puis avec la somme de 12 déterminants de matrice 2x2. Franchement je me vois pas calculer tout ça! c'est un effort assez colossale sans compter qu'on devra trouver une racine d'un polynome de degré 4.

(c'est une bonne idée de s'instruire sur le groupe des permutations )

[Lostounet]

Salut,

Que penses-tu des opérations élémentaires?

Du style C1 <= C1 - 2C3
Cela te fera apparaitre quelques zéros

Edit: je viens de voir qu'il y a deux colonnes identiques... donc le det vaut 0!

[vejitoblue]

oui j'y ai pensé, mais justement je sais pas si ça change le determinant.

edit: je cherche det(MATRICE-XI)

[Lostounet]

Euh.. déjà non, il y a un certain nombre d'opérations qu'on peut faire qui conservent le déterminant. Tu n'as pas vu ça? Que le det est une forme n linéaire alternée et qu'on peut le développer de plusieurs manières?

Mais ici tu as deux colonnes liées (en fait égales) donc la discussion est finie: det = 0

[vejitoblue]

salut, j'ai peut être pas été assez clair, je cherche det(A-XI), mais oui on peut toujours faire apparaitre des zeros!

[aviateur]

J'ai pas lu ce qu'il y a au dessus
mais tu peux faire ajouter ligne4 à ligne 2 et 3...

[vejitoblue]

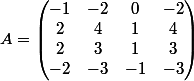
pour en revenir à celle là
donc chi(x)=-x(x+1)(x-1)² (j'ai trouvé un site qui calcule des trucs de ouf)
A priori c'est aussi le polynome minimal qui n'est pas scindé à racines simples, c'est à dire que A n'est pas diagonalisable
par contre elle est trigonalisable

sans faire de calculs (pas chercher les matrices de passage et son inverse, ni les vecteurs propres):
la matrice semblable à A serait de la forme :


il y a un moyen de trouver " ? " !=0 facilement

[sylvainc22]

Tu peux mettre n'importe quoi sauf 0. La preuve: pour la valeur propre 1, on a le système:

Av1 = 1v1
Av2 = ? v1 + 1v2 -> (A-1I)v2 = ? v1

Une fois que tu as v1, pour la ligne 2, tu résous le système pour trouver v2. Pour qu'il y ait une solution il faut que ?v1 soit dans Im(A-I). C'est le cas si v1 est dans Im(A-I) (en plus d'être dans ker(A-I) évidemment puisque c'est un vecteur propre de 1), et dans ce cas le plus simple est de prendre ? = 1 mais n'importe quel réel fait l'affaire.

[vejitoblue]

salut

(merci sylvain)

petit exo:

f un endomorphisme de E de dimension n et A la matrice de f
1)on suppose f de rang 1, quelle est la dimension du sous espace propre associée à la vp 0 ?
2)on note t la trace de A. mq t est valeur propre de f
3) mq le polynome caracteristique est chi(x)=(-1)^nX^n-1(X-t)
4) montrer que le polynome minimal est X (X-t)
5)montrer que f est diagonalisable ssi la trace de A est non nulle
6)soit v un vecteur non nul de Im(f). montrer que v est un vecteur propre de f asssocié à t

pour la 1) j'ai utilisé le théorème du rang:
dim(E)= rg(f)+ dim(ker(f))
mais ker(f) est l'espace propre associé à 0, du coup sa dimension est n-1

2)c'est assez visuel mais la preuve ça à l'air chiant. du coup on à une matrice A réduite par echelonnement à une matrice triangulaire par blocs du coup elle est semblable a une matrice triangulaire avec sur la diagonale n-1 zéro et un t donc t est valeur propre

3)A triangulaire =>chi(x)= (t-X)(-X)^n-1=-(x-t)(-1)^(n-1)(X)^(n-1) = ok

4)m(X)=X(X-t)
m(A)= A(A-tI)=0 (faut encore le prouver c'est encore "visuel" mais peut être en explicitant les coefficients de A(A-tI)) ça devrait marcher)
de plus le m(X) divise chi(X) (on peut faire une réccurence X^n(X-t)=X^(n-1)(X-t)X
m(X) est donc le polynome minimal (il divise chi annule f et est sous forme produit (X-vp))

je réfléchis à la suite, mes preuves sont nulles (inexistantes même) mais le plus important pour l'instant c'est de comprendre, les formalités plus tard

++