Bonjour !
J'aimerais avoir un renseignement pour cet exo :
Soit q un réel différent de 1. Démontrer que pour tout n entier naturel, la somme de k=0 à n de kq^k = (1-(n+1)q^n+nq^(n+1))/(1-q²) * q.
J'ai fait l'initialisation ok
Par contre pour l"hérédité :
J'ai donc écrit : je cherche la somme de k=0 à n+1 de kq^k = (q-(n+2)q^(n+2) + (n+1)q^(n+3))/(1-q)² après calcul.
et ensuite je dois donc écrire autrechose pour montrer l'hérédité à savoir somme de k=0 à n+1 de kq^k+... et je ne sais pas quoi justement
Merci de m'expliquer
Récurrence et somme
4 messages
- Page 1 sur 1
Bonsoir
Il existe un démonstration directe du résultat en écrivant:
=\sum_{k=0}^nkq^k=\sum_{k=1}^nkq^k=q\sum_{k=1}^n kq^{k-1}) et en remarquant que
et en remarquant que 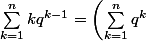') , la dérivée étant prise bien entendu par rapport à q.
, la dérivée étant prise bien entendu par rapport à q.
}{1-q})
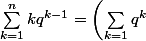'=\left(\dfrac{q(1-q^n)}{1-q}\right)')
=q\left(\dfrac{q(1-q^n)}{1-q}\right)')
Le calcul de la somme est alors ramené au calcul de dérivée ( vérifier que la formule trouvée reste valable pour q=1)
Remarque: Le dénominateur ne serait -il pas (1-x)² au lieu de 1-x²?
pluie2 a écrit:en fait j'ai trouvé j'ai ajouté (n+1)q^(n+1) et ça marche
Il existe un démonstration directe du résultat en écrivant:
Le calcul de la somme est alors ramené au calcul de dérivée ( vérifier que la formule trouvée reste valable pour q=1)
Remarque: Le dénominateur ne serait -il pas (1-x)² au lieu de 1-x²?
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
