Récurrence homogène
30 messages
- Page 1 sur 2 - 1, 2
Récurrence homogène
Bonjour, j'aurais besoin d'un coup de main quand à la résolution de ces deux questions.
1- Trouver la solution de la récurrence homogène U_k=U_k-1 + 2U_k-2 avec les conditions initiales
U_0 = 1
U_1 = 2
2 - Trouver la solution exacte de la récurrence U_k= 2U_k-1 +2^k avec la condition
U_0=1
En déduire la solution de la récurrence T(n)=2T(n/2)+n avec la condition T(1)=1
Pourriez vous m'indiquer la marche à suivre pour résoudre ce problème ?
1- Trouver la solution de la récurrence homogène U_k=U_k-1 + 2U_k-2 avec les conditions initiales
U_0 = 1
U_1 = 2
2 - Trouver la solution exacte de la récurrence U_k= 2U_k-1 +2^k avec la condition
U_0=1
En déduire la solution de la récurrence T(n)=2T(n/2)+n avec la condition T(1)=1
Pourriez vous m'indiquer la marche à suivre pour résoudre ce problème ?
Cette histoire est entièrement vraie puisque je l'ai inventé du début à la fin !
zygomatique a écrit:salut
1/ poseet cherche les réels r qui conviennent ...
Je me rappelle vaguement d'avoir fait ce genre de choses en physique l'an dernier pour résoudre des équa diff notamment il me semble. Mais c'est un peu loin.
J'avoue ne pas comprendre pourquoi l'on pose ceci, comment peut on savoir que u_k est de la forme e^kr
Merci de votre aide !
Cette histoire est entièrement vraie puisque je l'ai inventé du début à la fin !
J'ai eu beau chercher je ne comprends toujours pas comment l'on peut en arriver à émettre l'hypothèse Uk=e^kr
Une fois qu'on a l'expression de Uk le taf est terminé ça devient une équation simple; mais là la seule chose que l'on sait sur Uk ce sont les deux valeurs de conditions initiales et son expression en fonction de Uk lui même. :mur:
Une fois qu'on a l'expression de Uk le taf est terminé ça devient une équation simple; mais là la seule chose que l'on sait sur Uk ce sont les deux valeurs de conditions initiales et son expression en fonction de Uk lui même. :mur:
Cette histoire est entièrement vraie puisque je l'ai inventé du début à la fin !
En fait tu dois chercher une suite solution "simple" de la forme 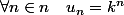
"Remplace" les termes par leurs valeurs respectives, et tu tombe sur ce qu'on appelle l'équation caractéristique de ta relation de récurrence. Selon le discriminant de l'équation caractéristique, les racines te définissent les solutions de ton problème.
par leurs valeurs respectives, et tu tombe sur ce qu'on appelle l'équation caractéristique de ta relation de récurrence. Selon le discriminant de l'équation caractéristique, les racines te définissent les solutions de ton problème.
Si tu as des notions d'algèbre linéaire sur les espaces vectoriels, l'espace des suites vérifiant ta relation est de dimension 2. Il faut donc que tu trouve une base de suites vérifiant la relation, et alors tu peux écrire toute suite vérifiant ta relation sous la forme
de suites vérifiant la relation, et alors tu peux écrire toute suite vérifiant ta relation sous la forme 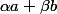 avec des constantes
avec des constantes  et
et  quelconques. Le plus naturel étant de prendre des suites simples, comme celle que je t'ai proposé au début. La suite exponentielle fonctionne aussi, c'est juste une question de choix ^^
quelconques. Le plus naturel étant de prendre des suites simples, comme celle que je t'ai proposé au début. La suite exponentielle fonctionne aussi, c'est juste une question de choix ^^
Les "conditions initiales" ont pour but de fixer une unique solution, comme dans les problèmes de Cauchy (Les deux relations vont fixer tes deux constantes et
et 
"Remplace" les termes
Si tu as des notions d'algèbre linéaire sur les espaces vectoriels, l'espace des suites vérifiant ta relation est de dimension 2. Il faut donc que tu trouve une base
Les "conditions initiales" ont pour but de fixer une unique solution, comme dans les problèmes de Cauchy (Les deux relations vont fixer tes deux constantes
Même si ça reste un peu abstrait, en me parlant de base, j'ai compris qu'on cherchait une famille de fonction.
Partant de cette hypothèse je pense donc que travailler avec Uk=e^rk est plus simple.
U0=1 avec r=1 ça marche.
U1=2 différent de e^1 du coup ça marche pas ...
Comment doit on faire au final ?
Partant de cette hypothèse je pense donc que travailler avec Uk=e^rk est plus simple.
U0=1 avec r=1 ça marche.
U1=2 différent de e^1 du coup ça marche pas ...
Comment doit on faire au final ?
Cette histoire est entièrement vraie puisque je l'ai inventé du début à la fin !
Si on note  l'espace vectoriel des suites vérifiant ta relation de récurrence, on a
l'espace vectoriel des suites vérifiant ta relation de récurrence, on a  . Pour résoudre ton problème, on va chercher la forme générale d'une suite vérifiant ta relation de récurrence, puis on déterminera les valeurs exactes des paramètres pour lesquelles tes deux conditions sur
. Pour résoudre ton problème, on va chercher la forme générale d'une suite vérifiant ta relation de récurrence, puis on déterminera les valeurs exactes des paramètres pour lesquelles tes deux conditions sur  et
et  sont vérifiées ^^
sont vérifiées ^^
Tu sais qu'en dimension finie il existe nécéssairement une base de ton espace vectoriel de tes solutions, il s'agit d'une famille libre de deux suites qu'on notera et
et  . La donnée de ces deux suites est suffisante pour pouvoir exprimer toute solution de ton problème sous la forme :
. La donnée de ces deux suites est suffisante pour pouvoir exprimer toute solution de ton problème sous la forme :
 \in \mathbb{C}^2 ; \, u = \alpha a + \beta b)
N'importe quelle base conviendra ! Il suffit de trouver une famille libre de deux suites vérifiant ta relation. Une méthode commode pour trouver de telles suites consiste à chercher des solutions sous la forme
 avec
avec 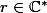 (la suite nulle n'a aucun intérêt elle ne peut pas contribuer a une base).
(la suite nulle n'a aucun intérêt elle ne peut pas contribuer a une base).
On se donne alors un entier et on cherche une condition pour qu'une telle suite vérifie la relation : tu remplace dans la relation de récurrence et tu arrives a (
et on cherche une condition pour qu'une telle suite vérifie la relation : tu remplace dans la relation de récurrence et tu arrives a (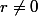 ) :
) :
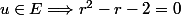
La résolution de cette équation te donne :
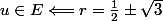
Tu en déduis donc les deux suites :
^n \quad ; \quad b_n = (\frac{1}{2} - \sqrt{3})^n)
(Vérifie que les suites sont linéairement indépendantes pour te convaincre que c'est bien une base ^^)
et donc l'expression générale d'une suite vérifiant la relation de récurrence (vérifie aussi la réciproque) :
 \in \mathbb{C}^2 \forall n \in n u_n = \alpha (\frac{1}{2} + \sqrt{3})^n + \beta (\frac{1}{2} - \sqrt{3})^n)
Puis pour trouver les deux constantes et
et  tu as juste a utiliser tes conditions initiales ^^
tu as juste a utiliser tes conditions initiales ^^
EDIT : Pour l'analogie avec les équations différentielles : Si un problème de Cauchy est donné sous la forme :
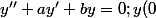=\alpha ; y'(0)=\beta)
L'espace vectoriel des solutions est de dimension 2 aussi. Ainsi, tu cherche une base de cet espace des solutions pour exprimer toutes les fonctions solutions de l'équation différentielle. On cherche ces solutions sous une forme qui nous arrange, i.e.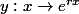 et on cherche une condition sur
et on cherche une condition sur 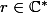 pour que la fonction choisie soit solution, ce qui donne les deux valeurs de
pour que la fonction choisie soit solution, ce qui donne les deux valeurs de  et ainsi une base de l'espace des solutions de l'équation. Reste a déterminer les constantes de "projection" grâce aux conditions initiales (Le problème de Cauchy a une unique solution, c'est Cauchy-Lipschitz qui le dit ^^).
et ainsi une base de l'espace des solutions de l'équation. Reste a déterminer les constantes de "projection" grâce aux conditions initiales (Le problème de Cauchy a une unique solution, c'est Cauchy-Lipschitz qui le dit ^^).
Ce raisonnement avec l'algèbre linéaire est très général : On peut ainsi résoudre des problèmes de Cauchy de la forme :
y' + b(t)y = 0 ; y(0)=\alpha ; y'(0)=\beta) où a et b sont des fonctions ! L'espace vectoriel des solutions est toujours de dimension 2, il s'agit donc toujours d'en trouver deux (mais les chercher sous forme exponentielle ne marche plus toujours, il faut être plus inventif !) et vérifier qu'elles forment bien une base de l'espace des solutions.
où a et b sont des fonctions ! L'espace vectoriel des solutions est toujours de dimension 2, il s'agit donc toujours d'en trouver deux (mais les chercher sous forme exponentielle ne marche plus toujours, il faut être plus inventif !) et vérifier qu'elles forment bien une base de l'espace des solutions.
Tu sais qu'en dimension finie il existe nécéssairement une base de ton espace vectoriel de tes solutions, il s'agit d'une famille libre de deux suites qu'on notera
N'importe quelle base conviendra ! Il suffit de trouver une famille libre de deux suites vérifiant ta relation. Une méthode commode pour trouver de telles suites consiste à chercher des solutions sous la forme
On se donne alors un entier
La résolution de cette équation te donne :
Tu en déduis donc les deux suites :
(Vérifie que les suites sont linéairement indépendantes pour te convaincre que c'est bien une base ^^)
et donc l'expression générale d'une suite vérifiant la relation de récurrence (vérifie aussi la réciproque) :
Puis pour trouver les deux constantes
EDIT : Pour l'analogie avec les équations différentielles : Si un problème de Cauchy est donné sous la forme :
L'espace vectoriel des solutions est de dimension 2 aussi. Ainsi, tu cherche une base de cet espace des solutions pour exprimer toutes les fonctions solutions de l'équation différentielle. On cherche ces solutions sous une forme qui nous arrange, i.e.
Ce raisonnement avec l'algèbre linéaire est très général : On peut ainsi résoudre des problèmes de Cauchy de la forme :
Merci pour toutes ces explications.
A partir de la suite exprimé, trouver alpha et béta ne pose pas de problème.
En revanche, je n'ai toujours pas compris comment on en arrive là^^navré :mur:
Pour les racines de l'équation Ok. Mais comment as on posé à la base la dite équation
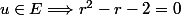
Si j'ai bien compris ça vient du fait que la dimension est 2 que notre polynôme est de degré 2. Mais ça ne me dit pas comment on arrive à dire que son expression exacte est celle là.
En fait en écrivant ceci je crois comprendre.
Tu vas me dire si j'ai tord ou pas.
U_k=U_k-1 + 2U_k-2
U_k - U_k-1 - 2U_k-2 = 0 (Équation homogène du coup)
Dimension 2 donc
r² - r^1 - 2r^0 = r²-r-2
Si c'est bien ça, il ne me reste plus qu'à comprendre une chose, comment sait on que la dimension de l'espace des suites vérifiant notre relation est bien 2 ?
Merci encore.
A partir de la suite exprimé, trouver alpha et béta ne pose pas de problème.
En revanche, je n'ai toujours pas compris comment on en arrive là^^navré :mur:
Pour les racines de l'équation Ok. Mais comment as on posé à la base la dite équation
Si j'ai bien compris ça vient du fait que la dimension est 2 que notre polynôme est de degré 2. Mais ça ne me dit pas comment on arrive à dire que son expression exacte est celle là.
En fait en écrivant ceci je crois comprendre.
Tu vas me dire si j'ai tord ou pas.
U_k=U_k-1 + 2U_k-2
U_k - U_k-1 - 2U_k-2 = 0 (Équation homogène du coup)
Dimension 2 donc
r² - r^1 - 2r^0 = r²-r-2
Si c'est bien ça, il ne me reste plus qu'à comprendre une chose, comment sait on que la dimension de l'espace des suites vérifiant notre relation est bien 2 ?
Merci encore.
Cette histoire est entièrement vraie puisque je l'ai inventé du début à la fin !
L'équation caractéristique vient de la forme sous laquelle on recherche la base de suites solutions ! Si tu veux tu peux chercher des suites sous la forme
))
Mais je ne te garantis pas que tu trouveras des solutions (D'ailleurs tu n'en trouveras pas :zen: ) et imagine un peu les calculs...
La seule chose dont on a besoin c'est de deux suites solution. On a alors l'idée merveilleuse de prendre des suites de la forme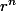 parce que ça a une bonne tête et c'est simple ^^
parce que ça a une bonne tête et c'est simple ^^
Du coup, supposons que notre suite de la forme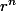 soit solution du problème. On a alors :
soit solution du problème. On a alors :
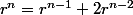
Ce qui revient a dire que, comme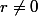 :
:
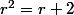
Ainsi, la suite qu'on a postulée peut être solution du problème ; a condition que r vérifie cette équation du second ordre ! Et il se trouve que cette équation nous fournit deux solutions, donc tu as trouvé deux suites différentes, solution du problème et linéairement indépendantes ; c'est à dire une base de ton espace de solution. Tu as donc terminé ^^
On aurait eu un problème si le discriminant de l'équation vérifiée par r était 0... On n'aurait eu qu'une seule suite et il nous en aurait manqué une. Dans ce cas il aurait fallu en chercher une deuxième en bidouillant. Ce qui marche bien c'est de prendre une suite btelle que, en notant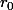 la solution double de l'équation précédente,
la solution double de l'équation précédente,
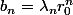
Et de chercher une relation de récurrence simple sur la suite , d'en déduire le terme général de cette suite et d'en déduire u ! (Essaye de faire les calculs pour t'entrainer, on trouve
, d'en déduire le terme général de cette suite et d'en déduire u ! (Essaye de faire les calculs pour t'entrainer, on trouve
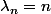 et donc
et donc 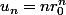
Et alors les solutions générales sont de la forme :
 r_0^n)
Mais je ne te garantis pas que tu trouveras des solutions (D'ailleurs tu n'en trouveras pas :zen: ) et imagine un peu les calculs...
La seule chose dont on a besoin c'est de deux suites solution. On a alors l'idée merveilleuse de prendre des suites de la forme
Du coup, supposons que notre suite de la forme
Ce qui revient a dire que, comme
Ainsi, la suite qu'on a postulée peut être solution du problème ; a condition que r vérifie cette équation du second ordre ! Et il se trouve que cette équation nous fournit deux solutions, donc tu as trouvé deux suites différentes, solution du problème et linéairement indépendantes ; c'est à dire une base de ton espace de solution. Tu as donc terminé ^^
On aurait eu un problème si le discriminant de l'équation vérifiée par r était 0... On n'aurait eu qu'une seule suite et il nous en aurait manqué une. Dans ce cas il aurait fallu en chercher une deuxième en bidouillant. Ce qui marche bien c'est de prendre une suite btelle que, en notant
Et de chercher une relation de récurrence simple sur la suite
Et alors les solutions générales sont de la forme :
Sur le "Pourquoi l'espace des solutions est de dimension 2", on raisonne en deux temps :
- Déja on montre que E est un sous espace vectoriel de l'espace des suites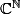 (Ca s'écrit tout seul)
(Ca s'écrit tout seul)
- On montre maintenant que toute famille libre de 2 vecteurs est génératrice, pour démontrer qu'il est de dimension 2. On se donne deux suites a et b dont on exige qu'elles vérifient la relation de récurrence et qu'elles soient linéairement indépendantes. On va montrer qu'on peut écrire toutes les solutions sur cette famille de suites.
Soit u une suite de E. Supposons qu'il n'existe PAS de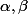 tels que
tels que 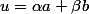 , donc que, pour tout n, on ne peut PAS écrire :
, donc que, pour tout n, on ne peut PAS écrire :
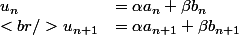
Seulement, ça revient a dire que le vecteur) est colinéaire au vecteur
est colinéaire au vecteur ) ("Ca ne se croise pas donc ya pas de solution"), et ainsi a est colinéaire a b, alors qu'on a supposé qu'elles étaient linéairement indépendantes --> Absurde !
("Ca ne se croise pas donc ya pas de solution"), et ainsi a est colinéaire a b, alors qu'on a supposé qu'elles étaient linéairement indépendantes --> Absurde !
Et donc la famille (a,b) est forcément une famille génératrice. On a montré que toute famille libre de deux suites de E est aussi une famille génératrice de E, ce qui revient a dire que E est de dimension 2.
- Déja on montre que E est un sous espace vectoriel de l'espace des suites
- On montre maintenant que toute famille libre de 2 vecteurs est génératrice, pour démontrer qu'il est de dimension 2. On se donne deux suites a et b dont on exige qu'elles vérifient la relation de récurrence et qu'elles soient linéairement indépendantes. On va montrer qu'on peut écrire toutes les solutions sur cette famille de suites.
Soit u une suite de E. Supposons qu'il n'existe PAS de
Seulement, ça revient a dire que le vecteur
Et donc la famille (a,b) est forcément une famille génératrice. On a montré que toute famille libre de deux suites de E est aussi une famille génératrice de E, ce qui revient a dire que E est de dimension 2.
Bonsoir,
Pour la méthode utilitariste à utiliser au jour le jour oui c'est bien ça, si Un = aUn-1 +bUn-2, on étudie le polynôme r^2-ar-b, et les solutions seront de la forme x.r1^n+y.r2^n, où r1 et r2 sont les deux racines du polynômes. Plus d'infos sur la méthode et les différents cas sur http://fr.wikipedia.org/wiki/Suite_r%C3%A9currente_lin%C3%A9aire#Suite_r.C3.A9currente_lin.C3.A9aire_d.E2.80.99ordre_2 par exemple.
Par contre en effet ça sort un peu du ciel "On a alors l'idée merveilleuse" présenté comme ça. On peut aussi poser le problème autrement et l'idée merveilleuse sera en fait une conséquence logique de la résolution :
On part de l'équation :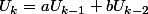
On aime pas ça parce que c'est de d'ordre deux alors on va essayer de se ramener à une autre suite récurrente d'ordre 1 que l'on saura résoudre. Pour ça, je pose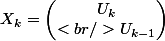
Si l'on essaye d'exprimer X_k en fonction de X_(k-1), on a tout simplement :

C'est à dire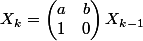
On s'est bien ramené à une suite géométrique d'ordre 1, mais matricielle ! Qu'à cela ne tienne, cela se comporte exactement comme dans R, et si on note A la matrice, on a :
C'est à dire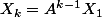
Comment calculer la puissance de A ? en la diagonalisant tout bêtement, si on trouve D la diagonale et P la matrice de passage, on aura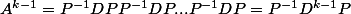
Or que sont les valeurs sur la diagonale ? Les valeurs propres de la matrice notées r1 et r2, qui annulent donc le polynôme caractéristique de la matrice A qui se trouve être le déterminant = (a-x)*(-x) - b*1 = x^2-ax-b)
Comme par hasard, on a retrouvé notre polynôme !
Si on réécrit la solution, on a donc en fait
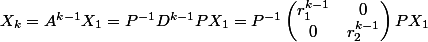
Partant de là, quelle que soit la tête de P et des conditions initiales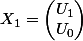 , on sait que les composantes de X_k seront forcément une combinaison linéaire des termes de notre diagonale, et donc que la solution U_k est une combinaison linéaire de
, on sait que les composantes de X_k seront forcément une combinaison linéaire des termes de notre diagonale, et donc que la solution U_k est une combinaison linéaire de 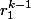 et
et 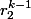 , ce qui est la même chose que de dire que c'est une combinaison linéaire de
, ce qui est la même chose que de dire que c'est une combinaison linéaire de 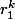 et
et 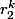 .
.
Pas de magie, pas d'astuce, tout s'explique !
Damien
Pour la méthode utilitariste à utiliser au jour le jour oui c'est bien ça, si Un = aUn-1 +bUn-2, on étudie le polynôme r^2-ar-b, et les solutions seront de la forme x.r1^n+y.r2^n, où r1 et r2 sont les deux racines du polynômes. Plus d'infos sur la méthode et les différents cas sur http://fr.wikipedia.org/wiki/Suite_r%C3%A9currente_lin%C3%A9aire#Suite_r.C3.A9currente_lin.C3.A9aire_d.E2.80.99ordre_2 par exemple.
Par contre en effet ça sort un peu du ciel "On a alors l'idée merveilleuse" présenté comme ça. On peut aussi poser le problème autrement et l'idée merveilleuse sera en fait une conséquence logique de la résolution :
On part de l'équation :
On aime pas ça parce que c'est de d'ordre deux alors on va essayer de se ramener à une autre suite récurrente d'ordre 1 que l'on saura résoudre. Pour ça, je pose
Si l'on essaye d'exprimer X_k en fonction de X_(k-1), on a tout simplement :
C'est à dire
On s'est bien ramené à une suite géométrique d'ordre 1, mais matricielle ! Qu'à cela ne tienne, cela se comporte exactement comme dans R, et si on note A la matrice, on a :
C'est à dire
Comment calculer la puissance de A ? en la diagonalisant tout bêtement, si on trouve D la diagonale et P la matrice de passage, on aura
Or que sont les valeurs sur la diagonale ? Les valeurs propres de la matrice notées r1 et r2, qui annulent donc le polynôme caractéristique de la matrice A qui se trouve être le déterminant
Comme par hasard, on a retrouvé notre polynôme !
Si on réécrit la solution, on a donc en fait
Partant de là, quelle que soit la tête de P et des conditions initiales
Pas de magie, pas d'astuce, tout s'explique !
Damien
Merci à tous pour ces explications.
Si j'ai bien compris pour la suite de la question 2.
On va chercher à résoudre l'équation suivante: r²-2r -2^k (mais là c'est fonction de k, on risque d'avoir des soucis pour l'étude ?
sa nous fait un discriminant (-2)²-4*1*(-2^k) avec k>=0
DU coup le discriminant va être positif si k est impair et négatif si k est pair....et ça me bloque ici.
Si j'ai bien compris pour la suite de la question 2.
On va chercher à résoudre l'équation suivante: r²-2r -2^k (mais là c'est fonction de k, on risque d'avoir des soucis pour l'étude ?
sa nous fait un discriminant (-2)²-4*1*(-2^k) avec k>=0
DU coup le discriminant va être positif si k est impair et négatif si k est pair....et ça me bloque ici.
Cette histoire est entièrement vraie puisque je l'ai inventé du début à la fin !
Doraki a écrit:A mon avis l'exo demande juste que tu calcules les 10 premires termes et que tu les regardes attentivement (si tu n'as jamais vu comment résoudre les suites récurrentes linéaires avant, on te demande pas de réinventer la méthode)
Le soucis c'est qu'en complexité, on a jamais vraiment eu de cours, du coup il est fort probable qu'on aurait du voir comment résoudre ce type de suite mais qu'on ne l'a jamais fait....merci les restrictions budgétaires et les profs forcés d'enseigner une matière qui n'est pas la leur...
Donc non je pense pas qu'il soit suffisant de calculer comme ça des termes.
Cette histoire est entièrement vraie puisque je l'ai inventé du début à la fin !
Par analogie avec les equations différentielles, si tu as une equation :
y'' + ay' + by = f(t)
L'equation homogène associée est
y'' + ay' + by = 0
Et la solution de la premiere equation est la somme de la solution générale de l'equation homogène et d'une solution particulière de l'equation a résoudre
Ici c'est pareil, l'equation que tu dois resoudre correspond a une suite récurrente linéaire d'ordre 1 à laquelle tu rajoute un second membre f_k = 2^k
y'' + ay' + by = f(t)
L'equation homogène associée est
y'' + ay' + by = 0
Et la solution de la premiere equation est la somme de la solution générale de l'equation homogène et d'une solution particulière de l'equation a résoudre
Ici c'est pareil, l'equation que tu dois resoudre correspond a une suite récurrente linéaire d'ordre 1 à laquelle tu rajoute un second membre f_k = 2^k
La solution donnée par fatal_error est la bonne, on peut la retrouver comme ça.
On cherche les suites u solution de
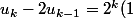)
D'après la théorie sur les suites récurrentes, on sait que l'ensemble des solutions de la relation 1 est constitué des suites de la forme u = a+b où :
- a est la solution générale de l'équation homogène :
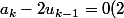)
- b est une solution particulière de l'équation (1).
- Résolution de (2) : On voit directement que a est une suite géométrique de raison 2 si elle est solution de l'équation (2) :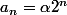
-Recherche d'une solution particulière de l'équation (1) : On utilise une méthode de la "variation des constantes", comme pour les équations différentielles. On ne veut qu'UNE SEULE solution de l'équation, on peut donc la chercher de la manière qu'on veut. Cherchons la sous la forme
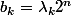 , car on peut voir que les choses vont se simplifier. On cherche alors une condition sur la suite
, car on peut voir que les choses vont se simplifier. On cherche alors une condition sur la suite  pour que b soit une solution de l'équation (1). Remplaçons dans l'équation (1) :
pour que b soit une solution de l'équation (1). Remplaçons dans l'équation (1) :
 2^k \\<br />& \Leftrightarrow \lambda_k = \lambda_{k-1} + 1 \\<br />& \Rightarrow \lambda_k = k<br />\end{array})
Tu as donc trouvé une suite lambda qui convient, et donc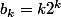 est une solution particulière de ton équation (1) (Vérifie le a la main ^^)
est une solution particulière de ton équation (1) (Vérifie le a la main ^^)
Ainsi, l'ensemble des solutions de l'équation (1) est constitué des suites de la forme
 2^k)
avec une constante a déterminer avec la valeur de u_0.
une constante a déterminer avec la valeur de u_0.
On cherche les suites u solution de
D'après la théorie sur les suites récurrentes, on sait que l'ensemble des solutions de la relation 1 est constitué des suites de la forme u = a+b où :
- a est la solution générale de l'équation homogène :
- b est une solution particulière de l'équation (1).
- Résolution de (2) : On voit directement que a est une suite géométrique de raison 2 si elle est solution de l'équation (2) :
-Recherche d'une solution particulière de l'équation (1) : On utilise une méthode de la "variation des constantes", comme pour les équations différentielles. On ne veut qu'UNE SEULE solution de l'équation, on peut donc la chercher de la manière qu'on veut. Cherchons la sous la forme
Tu as donc trouvé une suite lambda qui convient, et donc
Ainsi, l'ensemble des solutions de l'équation (1) est constitué des suites de la forme
avec
30 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
