Récurrence Forte
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Jean-Sebas
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Oct 2011, 05:31
-
 par Jean-Sebas » 09 Sep 2012, 12:24
par Jean-Sebas » 09 Sep 2012, 12:24
Coucou les gens

Voilà j'ai une récurrence forte à faire. Mais je ne comprends strictement rien à comment l'aborder. Et je peux même pas faire de corrélation avec les élément de l'énoncé.
Voilà :
On sait (cf. cours) que pour tout

:
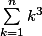
=
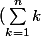^2)
.
On veut montrer que la suite des entiers est la seule suite de nombres strictement positifs vérifiant cette propriété.
Soit
_{k \ge 1})
une suite de
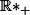
. On suppose que pour tout entier
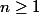
, on a l'égalité :
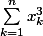
=
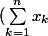^2)
.
Montrer, à l'aide d'une récurrence forte, que pour tout

, on a
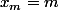
.
Merci de m'aider

-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 12:48
par Luc » 09 Sep 2012, 12:48
Salut, comment procèdes-tu pour montrer une propriété P(m) pour tout m de
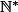
(ici,
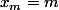
) par récurrence forte?
-
Jean-Sebas
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Oct 2011, 05:31
-
 par Jean-Sebas » 09 Sep 2012, 12:53
par Jean-Sebas » 09 Sep 2012, 12:53
Luc a écrit:Salut, comment procèdes-tu pour montrer une propriété P(m) pour tout m de
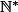
(ici,
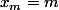
) par récurrence forte?
Euh bah d'abord
Initialisation : On montre que

est vraie ?
Mais comment ? Avec quoi ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 09 Sep 2012, 12:58
par Sylviel » 09 Sep 2012, 12:58
Ecris la propriété P1... est-elle vraie ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 12:59
par Luc » 09 Sep 2012, 12:59
Jean-Sebas a écrit:Euh bah d'abord
Initialisation : On montre que

est vraie ?
Exactement!
Jean-Sebas a écrit:Mais comment ? Avec quoi ?
Que signifie P(1) (avec des quantificateurs)? Est-elle vraie?
-
Jean-Sebas
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Oct 2011, 05:31
-
 par Jean-Sebas » 09 Sep 2012, 14:02
par Jean-Sebas » 09 Sep 2012, 14:02
En fait, je ne sais même pas ce qu'est

et encore moins l'hypothèse etc... L'énoncé me paraît très flou. Merci de m'éclairer
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 14:12
par Luc » 09 Sep 2012, 14:12
Jean-Sebas a écrit:En fait, je ne sais même pas ce qu'est

et encore moins l'hypothèse etc... L'énoncé me paraît très flou. Merci de m'éclairer
Salut,
avec les notations de l'exercice ce n'est pas

mais
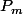
ou encore
)
. Et je l'ai écrite dans mon post précédent.
-
Jean-Sebas
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Oct 2011, 05:31
-
 par Jean-Sebas » 09 Sep 2012, 14:34
par Jean-Sebas » 09 Sep 2012, 14:34
D'accord
Donc je fais l'initialisation au rang 1 :

=1
Mais comment trouver la justification ?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 14:43
par Luc » 09 Sep 2012, 14:43
Jean-Sebas a écrit:D'accord
Donc je fais l'initialisation au rang 1 :

=1
C'est ce que tu veux montrer.
Jean-Sebas a écrit:Mais comment trouver la justification ?
Qu'est-ce que lénoncé suppose sur la suite
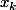
?
-
Jean-Sebas
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Oct 2011, 05:31
-
 par Jean-Sebas » 09 Sep 2012, 15:29
par Jean-Sebas » 09 Sep 2012, 15:29
Donc on a : x1 = 1 vraie
car 1 appartient a l'ensemble des reels positifs non nul.
C'est bien ca ? Merci.
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 16:40
par Luc » 09 Sep 2012, 16:40
Jean-Sebas a écrit:Donc on a : x1 = 1 vraie
car 1 appartient a l'ensemble des reels positifs non nul.
C'est bien ca ? Merci.
Non ce n'est pas ça. Il faut utiliser lhypothèse! Quelle est lhypothèse sur la suite
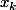
?
-
Jean-Sebas
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Oct 2011, 05:31
-
 par Jean-Sebas » 09 Sep 2012, 16:47
par Jean-Sebas » 09 Sep 2012, 16:47
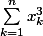
=
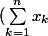^2)
Mais si on utilise cette hypothese, on a :
pour n =1, x1^3 = x1^2
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 16:52
par Luc » 09 Sep 2012, 16:52
Jean-Sebas a écrit: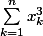
=
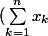^2)
Mais si on utilise cette hypothese, on a :
pour n =1, x1^3 = x1^2
Oui!
Et donc? quelles sont les valeurs possibles pour x1?
-
Jean-Sebas
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Oct 2011, 05:31
-
 par Jean-Sebas » 09 Sep 2012, 16:57
par Jean-Sebas » 09 Sep 2012, 16:57
Donc il faut faire une sorte de resolution d'equation ?
x1^3 = x1^2 <=> x1 = 1
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 16:59
par Luc » 09 Sep 2012, 16:59
Jean-Sebas a écrit:Donc il faut faire une sorte de resolution d'equation ?
x1^3 = x1^2 x1 = 1
C'est une résolution déquation.
Que penses-tu de 0^3=0^2=0?
-
Jean-Sebas
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Oct 2011, 05:31
-
 par Jean-Sebas » 09 Sep 2012, 17:07
par Jean-Sebas » 09 Sep 2012, 17:07
Ah oui je n'y ai pas pense ! Mais m n'est pas nul, non ? donc cette reponse n'est pas valide ?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 17:09
par Luc » 09 Sep 2012, 17:09
Jean-Sebas a écrit:Ah oui je n'y ai pas pense ! Mais m n'est pas nul, non ? donc cette reponse n'est pas valide ?
c'est quoi m?
-
Jean-Sebas
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Oct 2011, 05:31
-
 par Jean-Sebas » 09 Sep 2012, 17:14
par Jean-Sebas » 09 Sep 2012, 17:14
m appartient a l'ensemble des entiers naturels non nuls verifiant, Xm = m
Mais c'est plutot le fait que (Xk) est une suite de R positif etoile qui invalide la solution 0, c'est ca ?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 17:16
par Luc » 09 Sep 2012, 17:16
Jean-Sebas a écrit:m appartient a l'ensemble des entiers naturels non nuls verifiant, Xm = m
Mais c'est plutot le fait que (Xk) est une suite de R positif etoile qui invalide la solution 0, c'est ca ?
oui c'est ça.

est suppose strictement positif. Donc
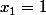
(les solutions de
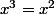
sont 0 et 1).
-
Jean-Sebas
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Oct 2011, 05:31
-
 par Jean-Sebas » 09 Sep 2012, 19:10
par Jean-Sebas » 09 Sep 2012, 19:10
Merci beaucoup pour votre aide. J'essayerai de faire la suite.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités