Recurrence fonctions iterees

par **andalous** » 23 Nov 2006, 20:36

salut voila j'ai 3 exos dont deux ou je bloque vraiment

l'exo sur les fonction iterees je sais vraiment pas comment faire. peut etre on peu montrer de suite la bijection ou alors passer par l'injectivité et la surjectivité.
l'exo sur fibonacci j'ai reussi jusqu'a la question 3 mais la 4 je n'y arrive pas
le dernier exo sur le nombre de surjectivité il me faudrait une piste pour démarrer
merci de m'aider bye

par **tize** » 23 Nov 2006, 20:43

bonsoir,
f est bijective si il existe g tel que fog=gof=IdE. Que peut on bien prendre pour g a ton avis ?

par **andalous** » 23 Nov 2006, 21:38

g= f^(n-1) car f^n = IdE donc f^(n-1)of = IdE et fof^(n-1) = IdE donc f bijective?!c bien sa

par **tize** » 23 Nov 2006, 21:39

Oui c'est bien ça...

par **andalous** » 23 Nov 2006, 21:52

ok merci pour ton aide. Je comprend la différence de l'expression pour la question d'aprés la valeur de n change selon celle de x non? mais alors je vois pas comment faire si on ne peu pas généraliser pour tout x

par **tize** » 23 Nov 2006, 21:59

f surjective n'est pas très dur...
f est injective si : f(x)=f(y) => x=y.

et

alors que peux tu dire de

et

?

par **andalous** » 23 Nov 2006, 22:32

oula je sais pas ce qu'on peut dire de f^(nm) mais peut etre de f^(m+n)???

par **tize** » 23 Nov 2006, 22:53

andalous a écrit:oula je sais pas ce qu'on peut dire de f^(nm) mais peut etre de f^(m+n)???

Oui c'est exact, c'est ce que je voulais dire... :we:
Pour la dernière, f est bijective et croissante donc strictement croissante, il suffit de regarder ce qu'il se passe sur {f(x)>x} et sur {f(x)<x}

par **andalous** » 23 Nov 2006, 23:20

on a f^(m+n)(x)= f^m(x)
f^(m+n)(y)= f^n(y)

donc f^(m+n)(x)=f^(m+n)(y) => f^m(x) = f^n(y) mais je vois pas ce qu'on peut dire de plus, je suis peut etre mal parti

par **andalous** » 23 Nov 2006, 23:54

et sinon pour la derniere question je vois pas comment prouver l'identité meme avec tes indications...

par **tize** » 24 Nov 2006, 09:39

Bonjour,

finalement, je reviens sur ce que j'ai dit pour l'affirmer...
on suppose

et

.
f envoie x sur x de manière périodique (tous les n itérées) donc pour tout multiple de n (par exemple avec p entier) on a aussi

.
De même avec y et m, on a pour tout entier p',

. Donc en prenant p=m et p'=n on a :

et

et comme

, on a aussi

.

par **tize** » 24 Nov 2006, 09:47

Je rappelle que f est bijective et croissante donc strictement croissante.
Pour la suite, on considère les ensembles

. Si A est non vide alors il existe

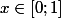
tq.

donc

et par récurrence pour tout

ce qui est contraire au hypothèses donc

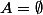
de même on montre que

donc pour tout

et

d'ou

par **tize** » 24 Nov 2006, 10:33

Dans l'exercice suivant, on montre facilement que

et puisque

on a aussi :

d'ou :

ce qui permet de conclure dans la dernière question via une série télescopique...

par **andalous** » 24 Nov 2006, 17:09

merci c'est beaucoup plus clair j'ai bien compris pour l'injectivité de l'identité dans l'exercice sur les iterees.
Par contre j'ai un probleme pour comprendre la question 4 de fibonacci.Avec tes indications du début j'arrive à F²n+1 - F²n - FnFn+1 = (-1)^n pour arriver à (-1)^n+1 je multiplie par -1 l'égalité mais ca me méne nul part il doit y avoir une autre astuce?...

par **andalous** » 25 Nov 2006, 00:50

personne peut m'expliquer davantage pour la question 4 de fibonacci. Je tourne en rond en remplacant Fn ou Fn+1 avec toutes les formules que j'ai mais je n'arrive au meme résultat tize!

par **tize** » 25 Nov 2006, 10:21

andalous a écrit:personne peut m'expliquer davantage pour la question 4 de fibonacci. Je tourne en rond en remplacant Fn ou Fn+1 avec toutes les formules que j'ai mais je n'arrive au meme résultat tize!

C'est normal, moi non plus je n'y arrive plus, sans doute je me suis trompé la dernière fois :scotch:

par **andalous** » 25 Nov 2006, 10:43

oki c'est pas grave.A un moment j'ai Fn+1/Fn + Fn/Fn+1 +1 il me semble. Je dois pouvoir trouver quelque chose d'interressant

par **tize** » 25 Nov 2006, 10:44

ça y est j'ai retrouvé ! je te poste ça dans 1 min

par **tize** » 25 Nov 2006, 10:49

donc en factorisant :

et finalement en divisant :

d'ou la suite téléscopique ! :we:

par **tize** » 25 Nov 2006, 10:55

On a après simplification :

Recurrence fonctions iterees

recurrence fonctions iterees

Qui est en ligne