Reciproque

[pHoeniX86]

Bonjour,

J'aimerais savoir comment construire la réciproque de cette fonction f(m,n)=(1/2)*(m+n)*(m+n+1)+m

[Lierre Aeripz]

Pourquoi cherches-tu une réciproque ? Je ne pense pas qu'elle soit très intéressante à exprimer. Peut-être voudrais-tu d'autres bijections similaires avec une réciproque plus simple ?

[tize]

Bonjour,
si f(a,b)=M alors tu peux considérer a=max{ n; n(n+1)/2 <= M } et b=M-a

[Joker62]

C'est la fonction qui permet de dénombrer les éléments de NxN
Et je confirme qu'en effet la réciproque ne doit rien avoir de génial...

[pHoeniX86]

Je cherche à avoir la réciproque pour pouvoir créer un programme en calculant directement à partir du résultat de la fonction f(m,n), les différents couples solutions de la réciproque.
Contrainte imposée par mon exo. En effet, j'ai déjà fait un programme qui recherche les couples solutions de la réciproque. Mais l'exo spécifie qu'il faut calculer les couples solutions par le biais de la fonction inverse à celle que je vous ai donné.

Mais je ne suis pas contre des exemples plus simples me permettant de comprendre comment arriver à ma solution moi-même.

[tize]

Bonjour,
si f(a,b)=M alors tu peux considérer a'=sup{n; n(n+1)/2<=M}, b=M-a'(a'+1)/2 et a=a'-b

[pHoeniX86]

Je vais être casse pied mais auriez vous un exemple concret.

[tize]

Concrètement si M=1234
tu cherches a', ici a' vaut 49 car 49*50/2=1225
b=1234-1225=9
et a=49-9=40, on a bien f(a,b)=1234

[pHoeniX86]

Ok merci pour l'explication.
Dernières questions :
Comment sais tu comment calculer a' b et a? Est ce que ce sont les a' b et a de ma formule ou un simple exemple?
Comment trouves-tu la valeur 49?

[tize]

La seule difficulté consiste à trouver a', une fois que c'est fait, pour a et b c'est facile il suffit d'utiliser les formules que j'ai écrit dans le post #5.
Pour trouver a'=sup{n; n(n+1)/2<=M} tu te sers de la définition de celui-ci...
tu peux essayer tous les entiers n (en commençant par 0,1,2,3,...) tels que n(n+1)/2<=M=f(a,b); a' sera le plus grand de ceux-ci (ça c'est la méthode pas très intelligente et bourrin)
Tu peux aussi résoudre et prendre le premier entier inférieur ou égal à la racine positive.
Pour M=1234, l'équation devient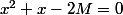 ou x^2+x-2468, la racine positive est 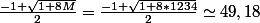donc a'=49

[pHoeniX86]

Merci pour ta patience et la clarté de tes explications.
La définition de a' mis à part l'égalite que tu as mise, je ne vois pas comment définir a'...
La question que je me pose c'est : Est ce que dans tous les cas où je voudrais calculer une réciproque avec des equations différentes, l'équation de a' sera la même?