[Optimisation] Rechercher le minimum d'une fonction à trois variables

[Tigereyes]

Bonjour alors j'ai un problème d'optimisation à résoudre mais je ne sais pas comment débuter car dans le cours c'est vraiment expliquer de manière générale et j'arrive pas à projeter les méthodes pour trouver le minimum de la fonction suivante :

f(x,y,x) = x² + (x-y)²+3(y-z)²-2x+6y-6z

Pouvez-vous me donner une piste, un indice pour pouvoir débuter?

Merci beaucoup à celles ou ceux qui daigneront me répondre :)

[busard_des_roseaux]

Il y a plusieurs aspects


i) c'est absolument certain que cette fonction admet un minimum absolu
(tend vers l'infini en dehors d'un compact de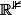

après on peut proposer:


ii) décomposition canonique du trinome; il suffit de développer
et de "ramasser" tout les monômes qui ont de la variable , dans un carré,
puis d'itérer avec y et z

Il m semble que ça s'appelle "décomposition de Gauss d'une forme quadratique"

peut être ainsi on trouve une somme de trois carrés qui est minimale à l'intersection
de trois hyperplans

iii)
l'analyse
calculer la différentielle et ses coordonnées dans la base (dx,dy,dz)
annuler
calculer la matrice hessienne

[busard_des_roseaux]

Pour la méthode (1), ça marche bien:

il suffit de faire trois décompositions canoniques de trinomes successives

a) avec tout ce qui concerne x, puis ce qui concerne y puis z
on trouve



sauf erreur de calcul

ce qui donne existence et unicité d'un minimum

b)
pour la méthode (ii) commencer à calculer les dérivées partielles

[Tigereyes]

Donc ici le minimum sera pour les trois composantes égales à

x = (y+1)/2

y= 1/13

z= 3

Merci beaucoup, j'étais parti sur la méthode du simplex mais c'est utiliser un char d'assaut pour tuer une mouche :briques: