Recherche d'une suite auxiliaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Sep 2010, 19:57
par Dinozzo13 » 30 Sep 2010, 19:57
Bonjour, soit la suite
)
définie sur

par

.
J'aimerais savoir quelle est la forme de la suite auxiliaire à introduire pour pouvoir exprimer
)
en fonction de

.
Exemple : Pour la suite
)
définie sur

par

, il faut déterminer le réel
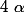
tel que la suite
)
:

soit géométrique.
Merci d'avance.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 30 Sep 2010, 20:22
par Pythales » 30 Sep 2010, 20:22
Il faut chercher les éléments invariants

et

racines de

et chercher

tel que
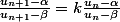

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 30 Sep 2010, 20:22
par Sa Majesté » 30 Sep 2010, 20:22
Salut
Tu peux t'amuser à introduire la suite
)
définie sur

par

et trouver des conditions sur
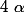
et sur

pour que
)
soit une suite géométrique
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Sep 2010, 20:28
par Dinozzo13 » 30 Sep 2010, 20:28
ok, je vais essayer ta méthode qui me semble plus simple, je vous tiens au courant :++:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 30 Sep 2010, 20:31
par benekire2 » 30 Sep 2010, 20:31
Salut, ce sont les mêmes méthodes dinno , simplement que la première te dit où donner de la tête.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Sep 2010, 20:39
par Dinozzo13 » 30 Sep 2010, 20:39
Voilà ce à quoi j'arrive :


-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 30 Sep 2010, 20:53
par Sa Majesté » 30 Sep 2010, 20:53
Dinozzo13 a écrit:Voilà ce à quoi j'arrive :

:ptdr: :marteau: :hein:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 30 Sep 2010, 21:14
par benekire2 » 30 Sep 2010, 21:14
Tu es spur que t'as essayé la toute première méthode ??
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 01 Oct 2010, 13:13
par Pythales » 01 Oct 2010, 13:13
Si
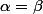
il faut mettre la relation sous la forme

-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 02 Oct 2010, 20:48
par Dinozzo13 » 02 Oct 2010, 20:48
Donc

est sous quelle forme ?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 02 Oct 2010, 20:51
par Sa Majesté » 02 Oct 2010, 20:51
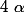
et

sont solutions de l'équation du second degré cx²+(a-d)x-b=0
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 02 Oct 2010, 21:00
par Dinozzo13 » 02 Oct 2010, 21:00
ouf !
Et comment puis-je en déduire une forme de v_n ?
Il faut que je dissocie tous les cas ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités