Recherche de limite ...

par **ben_michao** » 01 Oct 2006, 19:05

Bonjour atous, je suis a la recherche d'une limite et ca fait des heures que je suis dessus, si quelqun peut m'aider la voici :

lim(x-> +infini) x^(1+1/x) -x

Merci a tous

par **tize** » 01 Oct 2006, 19:32

cela revient à chercher la limite en 0 de :

sachant que

(si je dis pas de bêtise) tend vers 1 en 0, la fonction

peut être prolongée en 0 par 1 et donc trouver la limite en 0 de

revient à trouver la dérivée en 0 de

par **yos** » 01 Oct 2006, 19:32

Et tu fais un DL de l'exponentielle.

par **yos** » 01 Oct 2006, 19:34

Bon, Tize m'a précédé. Te voilà avec deux réponses, bon courage.

par **ben_michao** » 01 Oct 2006, 19:47

Tize je ne comprend pas ton histoire de derivée, qu'est ce que ca vient faire dans une recherche de limite ? que veut dire "peut etre prolongée en 0 " ?et si on remplace (1/u)^u par 1 , alors le quotient fait 0/0+ et c'est une forme indeterminée encore une fois !!!

Yos ,je voudrai resoudre cette limite sans les developpements limités car je ne suis pas censé en avoir besoin pour la resoudre.

Merci si vous pouvez m'eclaircir sur ces points

par **tize** » 01 Oct 2006, 19:54

donc

car h(0)=1

et calculer la limite de ceci en 0 revient (cours de terminale je crois ou premiere) à calculer

Il est dommage que tu ne puisses pas utiliser les DL car la méthode de Yos est beaucoup plus directe...
Cordialement José

par **ben_michao** » 01 Oct 2006, 20:28

Merci beaucoup pour ton aide tize, mais je n'arrive a pas a deriver h(u), sa forme est un peu compliquée avec sa variabe x... Si tu as une astuce !

par **yos** » 01 Oct 2006, 22:20

Pour Tize : est-ce qu'on ne tourne pas en rond avec ta méthode, car ta fonction est prolongée en 0 et donc pour étudier la dérivabilité, on doit chercher la limite du taux d'accroissement ? (à moins d'avoir un théorème de prolongement de la dérivée, mais ça me parait pas adapté pour ben michao si on n'a droit à rien).
On peut adapter ta méthode cependant :

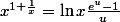, avec

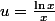qui tend vers 0.
Donc

tend vers 1 (limite connue en terminale ou bien on le retrouve par la définition du nombre dérivé de exponentielle en 0).
Après c'est facile.

par **tize** » 02 Oct 2006, 11:26

Voilà ce que je voulais faire :

et

mais effectivement Yos tu as à raison, à moins de savoir que l'on peut prolonger la dérivée en 0 de manière continue on tourne en rond...
merci pour ta remarque instructive, je tâcherai de faire plus attention la prochaine fois...

Cordialement
José

Recherche de limite ...

Recherche de limite ...

Qui est en ligne