Recherche d'un delta
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nico2b
- Membre Relatif
- Messages: 271
- Enregistré le: 16 Jan 2007, 17:33
-
par nico2b » 12 Mar 2007, 16:37
Bonjour... Voici l'énoncé : Soit
Définissez "f est continue en a" en temre de 
.
 - f(a) | \leq \epsilon)
Utilisez cette définition pour montrer que la fonction 
est continue en tout point a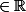
Il faut donc prouver : 
Voici la strucure de ma preuve...
Soit
>0.
Prenons
= ........
Soit x
Dom f tq |x-a|
Montrons que
.
En effet, on a que
= |(x-a)(x+a)| = |x-a||x+a|
.
.
.
Mais je n'arrive pas à trouver
Merci de votre aide...
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 12 Mar 2007, 17:39
Bonjour,
c'est de la continuité en a, ton delta dépend donc de epsilon et de a...
-
nico2b
- Membre Relatif
- Messages: 271
- Enregistré le: 16 Jan 2007, 17:33
-
par nico2b » 12 Mar 2007, 18:01
oui ça daccord mais je ne voit pas comment m'en sortir avec |x-a||x+a|...
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 12 Mar 2007, 18:09
Oui c'est pas évident. Avec
)
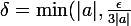, ça doit aller. Et encore il faut mettre le cas a=0 de côté.
-
nico2b
- Membre Relatif
- Messages: 271
- Enregistré le: 16 Jan 2007, 17:33
-
par nico2b » 12 Mar 2007, 18:25
merci et tu pourrais m'expliquer les détails pour trouver delta?
MErci
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 12 Mar 2007, 18:54
Ben tu veux
en partant d'une majoration de |x-a| seulement. Il faut donc que cette dernière entraîne une majoration de |x+a|.
L'idée est que pour x assez proche de a, tu as
proche de
D'où mon idée de le majorer par |3a|. Ce sera bon pour
car alors
.
En résumé il me faut
et
, d'où mon choix.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 12 Mar 2007, 18:55
Un peu nulle mon explication. Tize, fait quelquechose.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 90 invités
