Réccurence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
par nanard270227 » 26 Sep 2019, 18:13
Bonjour,
Pouvez-vous m'aider à résoudre cette récurrence svp ? Je sors de BTS et intègre une école d'ingénieur depuis la rentrée. De ce fait j'ai de grosses lacunes en maths par rapport aux autres élèves.
L'exercice est en image attachée.
PS : Je ne sais pas pourquoi, mais je n'arrive pas a intégrer ma formule sur cette page :
}{2(n+1)+1})
edit: ajout des balises [ tex] [/tex] autour de la formule
fatal_error
par nanard270227 » 26 Sep 2019, 18:16
Montrer que ∀n ∈N/ {0;1}→∑(k=1),(n) 1/k²>3n/(2n+1)
-
Vincoux
- Messages: 6
- Enregistré le: 26 Sep 2019, 15:53
-
par Vincoux » 26 Sep 2019, 18:35
Bonjour Nanard,
Commence par dire que la propriété est vraie à un certain rang (prenons 2 par exemple)
\over 2(2+1)+1})
vraie
Ensuite, nous supposons que la propriété est vraie au rang n.
Tu pars de cette propriété pour prouver qu'elle est également vraie au rang n+1.
C'est gagné.
-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
par fatal_error » 26 Sep 2019, 18:47
slt,
Soit
l'hypothèse:
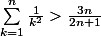
Soit
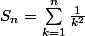
on veut montrer
(1):
^2} > \frac{3(n+1)}{2(n+1)+1})
une idée est de faire apparaitre
, de sorte qu'on puisse se servir de
}{2(n+1)+1} = \frac{3n + 3}{2n+3})
et on voudrait un truc genre
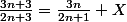
avec X à trouver
Si on remplace ensuite dans (1):
^2} > \frac{3n }{2n+1} + X)
il reste toujours à montrer que cette ineg est vraie
or
et si on montre que
^2} > X)
alors (1) est vraie et c'est g00d
la vie est une fête
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
