Rayon de CV
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 12 Fév 2010, 15:06
par Aspx » 12 Fév 2010, 15:06
Bonjour,
Je suis sur un exo de calcul de rayon de convergence et j'avoue qu'après avoir essayé puis cherché des réponses sur le net, j'ai pas trouvé grand chose sur le sujet.
Voici l'énoncé :
Calculer le RCV de la série

J'ai essayé d'appliquer les méthodes classiques style Hadamard en regroupant les termes nuls (n non carré parfait) et les

. On obtient pas de réponse car alors

tend soit vers zéro soit vers l'infini...
Merci par avance !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Fév 2010, 15:10
par Nightmare » 12 Fév 2010, 15:10
Salut !
Au choix, poser Z=z², voir ce qu'il se passe pour Z et repasser à z. Ou sinon, fixer z et voir ta série entière comme une série numérique.
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 12 Fév 2010, 15:17
par Aspx » 12 Fév 2010, 15:17
La méthode

s'applique bien si on avait du

mais là c'est

. Tu as surement mal lu ou alors je dois me tromper :marteau:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 12 Fév 2010, 15:29
par girdav » 12 Fév 2010, 15:29
Je pense que d'Alembert, moyennant un peu de travail sur les limites donne des trucs pas déguelasses.
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 12 Fév 2010, 15:45
par Aspx » 12 Fév 2010, 15:45
A l'aide de d'Alembert on montre que R = 0
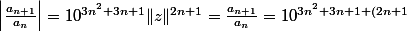\log{\|z\|}})
qui tend vers l'infini...
C'est bien ça ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Fév 2010, 15:45
par Nightmare » 12 Fév 2010, 15:45
Aspx a écrit:La méthode

s'applique bien si on avait du

mais là c'est

. Tu as surement mal lu ou alors je dois me tromper :marteau:
Oups oui désolé, je pensais que c'était 2n. Cela dit la méthode de fixer z convient par contre. :happy3:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 12 Fév 2010, 17:00
par girdav » 12 Fév 2010, 17:00
Aspx a écrit:A l'aide de d'Alembert on montre que R = 0
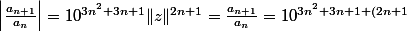\log{\|z\|}})
qui tend vers l'infini...
C'est bien ça ?
J'aurais plus écris que pour

on a que
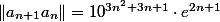\ln \|z\|})
. On ne regarde la limite que pour
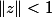
, sinon on aurait pu voir dès le départ que la série est grossièrement divergente dans ce cas.
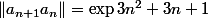\ln 10 +\(2n+1\)\ln |z \| \))
puis regarde la limite de ce qu'il y a dans l'exponentielle.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
